Решать задачу будем в два этапа: сначала определим число разбить друзей на 3 пронумерованные команды, а затем учтем, что эта нумерация не важна.
1. Формируем первую команду. Туда должны попасть некоторые 3 человека из 9. Порядок их выбора не важен, поэтому выбрать их можно 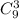 .
.
Формируем вторую команду. Туда должны попасть некоторые 3 человека из оставшихся 6. Порядок их выбора также не важен, поэтому выбрать их можно 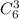 .
.
Оставшиеся 3 человека автоматически сформируют третью команду.
Поскольку каждому варианту первой команды можно поставить в соответствие 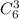 вариантов второй (и третьей) команды, то по правилу умножения всего разбить 9 человек на 3 пронумерованные команды:
вариантов второй (и третьей) команды, то по правилу умножения всего разбить 9 человек на 3 пронумерованные команды:
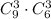
2. Теперь учтем тот факт, что у команд на самом деле нет номеров. Так как команд 3, то существует 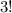 пронумеровать команды. Таким образом, количество непронумерованных вариантов разбиения в
пронумеровать команды. Таким образом, количество непронумерованных вариантов разбиения в 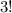 раз меньше, чем количество пронумерованных вариантов разбиения.
раз меньше, чем количество пронумерованных вариантов разбиения.
Значит, итоговое число разбить 9 человек на команды без учета их номеров:
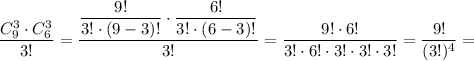
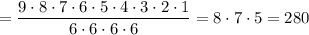
ответ: 280
Вторая сверху (№2)
Пошаговое объяснение:
I) 10 - 16,4 - (-20,6)-(-2,96) = 10 - 16,4 + 20,6 + 2,96 = -6,4 + 20,6 + 2,96 = 17,16
2) 20,5 - (-8,7) - (-15) - 18,5 = 20,5 + 8,7 + 15 - 18,5 = 44,2 - 18,5 = 25,7
3) 5,5 - (-10,24) - 13,3 - 17,3 = 5,5 + 10,24 - 13,3 - 17,3 = 15,74 - 13,3 - 17,3 = 2,44 - 17,3 = -14,86
4) -21 - (-5,54) - 22,4 - 27,3 = -21 + 5,54 - 22,4 - 27,3 = -15,46 - 22,4 - 27,3 = -65,16
5) 15 - 27,4 - (-34.4) - 26,1 = 15 - 27,4 + 34,4 - 26,1 = -12,4 + 34,4 - 26,1 = 22 - 26,1 = -4,1
Если перед скобкой стоит знак "-", то знак в скобке меняется на противоположный.
Наибольшее значение получилось во 2 цепочке 25,7. Оно наибольшее, т.к любое положительное число больше любого отрицательного.