1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
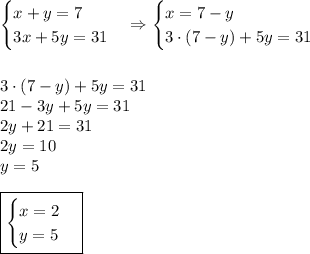 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
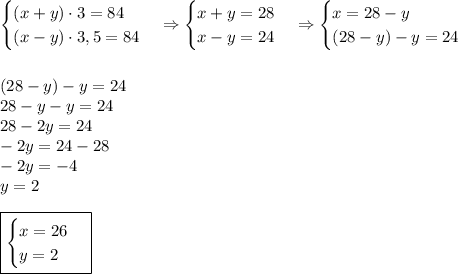
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке P. Найдите площадь параллелограмма, если BC = 12, а расстояние от точки P до стороны AB равно 9.
Решение
P — точка пересечения биссектрис, PН — высота треугольника АPВ, MN — высота параллелограмма, проходящая через точку P.
Рассмотрим треугольники AHP и APN. Они прямоугольные, углы HAP и PAN равны, поскольку АP — биссектриса, сторона AP — общая, следовательно, треугольники равны. Тогда PN = PH = 9. Аналогично, равны треугольники BPH и BPM, откуда MP = PH = 9.
MN = PN+MP = 9+9 = 18.
Найдем площадь параллелограмма как произведение основания на высоту.
S = BC*MN =12*18 = 216
ответ: 216.