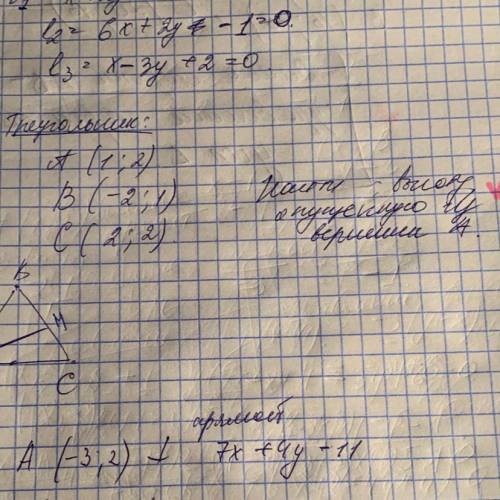
Можно найти площадь 2-ма складывания и вычитания:
складывания:
Разбиваем нашу фигуру на 2 прямоугольника:
2см на 6см
2см на 5см(6-1)
Теперь нужно посчитать их площади и добавить их
Площадь первого прямоугольника - 2см * 6см = 12см²
Площадь второго прямоугольника - 2см * 5см = 10см²
Площадь фигуры = 12см + 10см = 22см²
вычитания:
Посчитаем площадь фигуры вместе с пустотой размером 2см на 1см, а потом вычтем его из большого прямоугольника.
Площадь большого прямоугольника = 6см * 4см = 24см²
Площадь пустоты - 2см * 1см = 2см²
Площадь фигуры = 24см - 2 = 22см²
22м²
Пошаговое объяснение:
рис. 1 )
Найдем площадь всего прямоугольника и вычтем площадь не закрашенной части .
So- общая площадь фигуры
Sнз- площадь не закрашенной части
Sз - площадь закрашенной части
а= 4 м
b= 6 м
Sо=a*b= 6*4= 24 м²
с= 1 м
d= 2 м
Sнч= c*d= 1*2= 2 м²
Sз=So-Sнз
Sp= 24 - 2 = 22м²
рис. 2 )
Разделим закрашенную часть на две части
1-я часть прямоугольник со сторонами
а= 6-1=5 м
b= 4 м
2-я часть прямоугольник со сторонами
с= 1 м
d= 2 м
Тогда площадь закрашенной части фигуры будет :
S= (a*b) + ( c*d) = 5*4+2*1= 20+2= 22 м²
рис. 3)
Площадь закрашенной части состоит из двух прямоугольников
первый со сторонами
а= 2 м
b= 6 м
второй
с=5 м
d= 2 м
Сложим их площади и найдем площадь закрашенной части
S= (a*b)+ (c*d)= 2*6+5*2= 12+10 = 22 м²
рисунки во вложении
Дан треугольник АВС. Требуется найти высоту, опущенную из вершины А.
Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов.
Используя формулу S = ½ * |a × b|, вычислим площадь данного треугольника , где а = АВ = (-2 - 2; 1 – 1; 2 – (-3)) = (-4; 0; 5) и b = АС = (2 - 2; 4 – 1; 2 – (-3)) = (0; 3; 5).
Найдем векторное произведение векторов a и b: a × b = (0; 175; 0).
Тогда |a × b| = = √(0² + 175² + 0²) = 175.
Используя формулу определения расстояния между двумя точками, вычислим длину стороны ВС.
Имеем: ВС = √((2 – (-2))² + (4 - 1)² + (2 – 2)²) = √(4² + 3² + 0²) = √(25) = 5.
Как известно, площадь треугольника равна половине произведения основания на высоту.
Следовательно, высота опущенная из вершины А равна отношению удвоенной площади на основание ВС.
Имеем 2 * 87,5 / 5 = 175 : 5 = 35.
ответ: 35.