758. Запишите в виде дроби частное: 1) 4:12; 3) 16:8; 5) 12:23; 2) 6 : 25; 4) 14:23; 6) 17 : 11. 759. - id2080240720200110 от scorpziro 10.01.2020 19:41

Question

Математика: 758. Запишите в виде дроби частное: 1) 4:12; 3) 16:8; 5) 12:23; 2) 6 : 25; 4) 14:23; 6) 17 : 11. 759. Запишите в виде дроби частное: 1) 5 : 7; 3) 1:6; 5) 6 : 1; 2) 19:4; 4) 30 : 4; 6) 12:39. 7 17 760. Запишите дробь в виде частного: 1) ; 3) 17 12 584 29 761. Запишите дробь в виде частного: 1) , ; 2) ; 3) 10 5 11 ; 2) ; ) 3 ах

scorpziro · Accepted Answer

Переформулируем задачу следующим образом. Пусть один куст однозначно высаживается в первый день, один - во второй день, и один - в третий день.

Тогда, останется 7 кустов, которые распределить можно без каких-либо ограничений.

Для каждого из 7 кустов нам необходимо сделать выбор: в который из дней мы будем его высаживать: в первый, во второй или в третий. Повторения этих выборов допустимы (более того, в данном случае они гарантированно произойдут), порядок значения не имеет.

Значит, нам нужно вычислить такую конфигурацию, как число сочетаний с повторениями из 3 по 7.

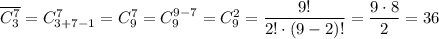
$\overline{C_3^7}=C_{3+7-1}^7=C_9^7=C_9^{9-7}=C_9^2=\dfrac{9!}{2!\cdot(9-2)!}=\dfrac{9\cdot8}{2} =36$

ответ

MOGZ ответил