Пошаговое объяснение:
№ 1
а) Маша идет со скоростью 5 км/ч,а Коля бежит со скоростью 10 км/ч.Во сколько раз коля двигается быстрее?
10 : 5 = 2 раза
Б) Машина ехала 4 часа со скоростью 80км/ч.какое расстояние она проехала?
4 * 80 = 320 км
в) Плот проплыл по течению реки 15 км за 5 часов.какова скорость течения реки?
15 : 5 = 3 км/ч
г) Корабль проплыл 120 км со скоростью 40 км/ч.Сколько времени он затратил?
120 : 40 = 3 часа
№ 2
вычисли 26 х (1672 + 1448) : (8713-8661) =м1560
1) 1672 + 1448 = 3120
2) 8713 - 8661 = 52
3) 26 * 3120 = 81120
4) 81120 : 52 = 1560
№ 3 из двух городов,расстояние между которыми 520 км одновременно вышли навстречу друг другу два поезда.Один поезд шёл со скоростью 60км/ч,а другой поезд со скоростью 70 км/ч. Через сколько часов встретятся поезда?
1) 60 + 70 = 130 км/ч скорость сближения
2) 520 : 130 = 4 часа
№ 4
переведите
300 см= 300 : 100 = 3 м,
25 000мм= 25000 : 1000 = 25 м,
2 мин= 2 * 60 = 120 с
5т 200 кг= 5200кг,
15дм= 1 м 5 дм,
350см= 3м 50 см
№ 5 запиши следующие числа в порядке возрастания 721163, 7211630, 72, 6262626, 626262 вычисли значение произведения самого маленького и самого большого из этих чисел столбиком.
72 , 626.262 , 721.163 , 6.262.626 , 7.211.630
7211630
* 72
1442326
+ 5048141
519237360
7.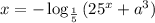
Пусть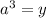 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию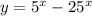 :
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно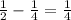 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,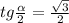
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем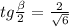
ответ: 4 : 3