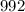 конфет он съедал по одной конфете из каждых семи.
конфет он съедал по одной конфете из каждых семи.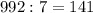 (остаток
(остаток 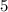 ), то Вася съел
), то Вася съел 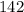 конфеты. После этого осталось
конфеты. После этого осталось 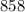 конфет.
конфет. 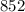 конфет он съедал по одной конфете из каждых девяти.
конфет он съедал по одной конфете из каждых девяти.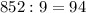 (остаток
(остаток 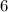 ), то Петя съел
), то Петя съел 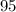 конфет.
конфет. Таким образом, осталось 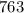 конфеты.
конфеты.
____
Если то не забывайте сказать " " на странице профиля. Успехов в учёбе!
Буду весьма признательна, если выберите мой ответ лучшим! Вам вернётся часть .
∠ABC = ∠BCD и ∠BAD = ∠ADC
По условию задания сказано, что ∠СAD=46°, а ∠BAС=1°.
∠BAD =∠СAD+∠BAС=46°+1°=47°.
∠BAD = ∠ADC=47°.
Сумма углов любого четырехугольника равна 360°
∠ABC + ∠BCD + ∠BAD+ ∠ADC =360°
47° + 47° + ∠BAD+ ∠ADC =360°
94° + ∠BAD+ ∠ADC =360°
∠BAD+ ∠ADC =360°-94°
∠BAD+ ∠ADC =266°
Поскольку ∠BAD = ∠ADC, то
∠BAD = ∠ADC=266°/2
∠BAD = ∠ADC=133°
ответ: большие углы равнобедренной трапеции ∠BAD = ∠ADC=133°