прямая BD перпендикулярна к плоскости треугольника ABC известно что BD равно 3 см АС равно 4 см BC равно Ba = 10 см Найдите расстояние от точки D до прямой AC B площадь треугольника ACD

👇

Увидеть ответ

Ответ:

anghelina1

22.05.2023

Подробное решение во вложении

прямая BD перпендикулярна к плоскости треугольника ABC известно что BD равно 3 см АС равно 4 см BC р

4,5(13 оценок)

Открыть все ответы

Ответ:

redle01

22.05.2023

Дробь называется правильной, если ее числитель меньше знаменателя. Если же числитель больше знаменателя или равен ему, то дробь называется неправильной.

Например, , , - правильные дроби, а , , - неправильные дроби.

Правильная дробь всегда меньше единицы.

Неправильная дробь обозначает число, большее или равное 1.

Например, < 1; > 1.

Дробь, у которой числитель равен знаменателю, равна 1.

Например, = 1.

Неправильную дробь часто записывают в виде смешанного числа - числа, состоящего из целой и дробной части.

Чтобы представить неправильную дробь в виде смешанного числа, нужно разделить с остатком числитель на знаменатель. Частное будет целой частью смешанного числа, остаток числителем дробной части, а делитель - знаменателем дробной части.

Пример: = 49 : 15 = 3 (ост. 4).

= 3

Чтобы представить смешанное число в виде неправильной дроби, нужно знаменатель умножить на целую часть числа, к полученному произведению прибавить числитель дробной части и записать эту сумму в числитель дроби. В знаменатель неправильной дроби записываем знаменатель дробной части смешанного числа.

Пример: 5 = = .

4,8(93 оценок)

Ответ:

Tanecka2501

22.05.2023

1) 2cos^2 x - 5sin x + 1 = 0
2 - 2sin^2 x - 5sin x + 1 = 0
-2sin^2 x - 5sin x + 3 = 0
2sin^2 x + 5sin x - 3 = 0
Квадратное уравнение относительно sin x
D = 5^2 - 4*2(-3) = 25 + 24 = 49 = 7^2
sin x = (-5 - 7)/4 = -12/4 = -3
Решений нет
sin x = (-5 + 7)/4 = 1/2
x = (-1)^k*pi/6 + pi*k

2) f(x) = (2x^3 - 1) / (2x^4 - 8)
f ' (x) = [6x^2*(2x^4 - 8) - (2x^3 - 1)*8x^3] / (2x^4 - 8)^2 =
= (12x^6 - 48x^2 - 16x^6 + 8x^3) / (2x^4 - 8)^2 = (-4x^6 + 8x^3 - 48x^2) / (2x^4 - 8)^2 = 0
Если дробь равна 0, то числитель равен 0, а знаменатель нет.
-4x^6 + 8x^3 - 48x^2 = 0
Делим всё на -4
x^6 - 2x^3 + 12x^2 = 0
а) x1 = x2 = 0; f(0) = (-1)/(-8) = 1/8
Но производная отрицательна и при x < 0, и при x > 0.
Поэтому x = 0 - критическая точка, но не экстремум, а точка перегиба.
Потому что в ней f '' (x) = 0

б) x^4 - 2x + 12 = 0
Это уравнение действительных корней не имеет

в) У функции ещё есть точки разрыва
2x^4 - 8 = 0
x^4 - 4 = 0
x1 = -√2
x2 = √2
Но производная все равно отрицательна при всех x, кроме точек разрыва.
ответ: функция убывает на всей области определения.

3) (2/3)^(2x+3) <= (9/2)^(x-2)
(2/3)^(2x) * (2/3)^3 <= (9/2)^x * (2/9)^2
(4/9)^x * 8/27 <= (9/2)^x * 4/81
(4/9 * 2/9)^x <= (4/81) * (27/8)
(8/81)^x <= 1/6
Основание 0 < 8/81 < 1, поэтому график убывает.
При переходе от степеней к показателям знак неравенства меняется
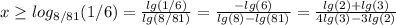
$x \geq log_{8/81} (1/6) = \frac{lg(1/6)}{lg(8/81)} = \frac{-lg(6)}{lg(8) - lg(81)}= \frac{lg(2)+lg(3)}{4lg(3)-3lg(2)}$

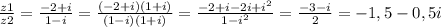
5) $\frac{z1}{z2}= \frac{-2+i}{1-i} = \frac{(-2+i)(1+i)}{(1-i)(1+i)} = \frac{-2+i-2i+i^2}{1-i^2}= \frac{-3-i}{2}=-1,5-0,5i$

6) f(x) = x^2 - 2x; x0 = 3
f(x0) = 3^2 - 2*3 = 9 - 6 = 3
f ' (x) = 2x - 2
f ' (x0) = 2*3 - 2 = 4
Уравнение касательной
y = f(x0) + f ' (x0)*(x - x0) = 3 + 4(x - 3) = 3 + 4x - 12
y = 4x - 9

4,4(20 оценок)

Это интересно:

Финансы-и-бизнес

21.12.2022

Как выбрать и купить восстановленный деревянный стол...

Компьютеры-и-электроника

18.01.2021

Как правильно пинговать IP адрес: простой гайд для начинающих...

Образование-и-коммуникации

26.01.2022

Как написать сочинение Как я провел лето : советы и рекомендации...

Финансы-и-бизнес