1)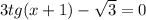
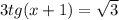
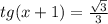
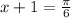
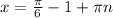
2)
3sin^2x+sinx*cosx-2cos^2x=0
Теперь делим все этоуравнение на cos^2x, получится:
3tg^2x + tgx - 2 = 0
tgx можно заменить на а(так легче решать просто):
tgx = a
3a^2 + a -2 = 0
И решаем квадратное уравнение:
D = 1^2 + 24 = 25
a1,2 = ( -1 +- 5 ) / 6 = > a1 = 2/3, a2 = -1 (эти числа подходят, т.к в тригонометрии промежуток идет от - 1 до 1, эти числа входят в этот промежуток)
Теперь, т.к мы делали замену tgx = a, то подставляем числа;
tgx = 2/3 => x = П/4 + Пn
tgx = -1 => x = arctg2/3 + Пn
1)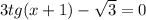
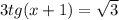
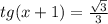
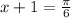
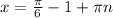
2)
3sin^2x+sinx*cosx-2cos^2x=0
Теперь делим все этоуравнение на cos^2x, получится:
3tg^2x + tgx - 2 = 0
tgx можно заменить на а(так легче решать просто):
tgx = a
3a^2 + a -2 = 0
И решаем квадратное уравнение:
D = 1^2 + 24 = 25
a1,2 = ( -1 +- 5 ) / 6 = > a1 = 2/3, a2 = -1 (эти числа подходят, т.к в тригонометрии промежуток идет от - 1 до 1, эти числа входят в этот промежуток)
Теперь, т.к мы делали замену tgx = a, то подставляем числа;
tgx = 2/3 => x = П/4 + Пn
tgx = -1 => x = arctg2/3 + Пn
если правая и левая чаши равны, то наша монета настоящая и на правой чаше весов тоже настоящая. Проводим ещё два взвешивания. Если ни одна из монет не равна нашей, то они фальшивые. Если одна равна нашей, то она настоящая, а оставшиеся две фальшивые.
если правая и левая часть не равны, то убираем любую монету. например оставляем тяжелую. проводим ещё два измерения. если обе монеты легче оставленной, то она фальшивая. если обе монеты такие же, то они все три настоящие.