Пошаговое объяснение:
Разобьём всех гномов по тройкам, чтобы найти сколько из них могут стоять между гномами в колпаках одного цвета:
105:3=35, а нужно 67. Значит надо добавить к 32 тройкам по гному в таком же колпаке. Получается 32 квартета одного цвета и 3 тройки:
3×3+32×4=137.
31 гном лишний, т. е. 8 квартетов подряд должны быть одного цвета. Остаётся 16 квартетов и 3 тройки, из которых две соседние тройки должны быть одного цвета. Итак имеем 8 соседних квартетов одного цвета, 2 соседних тройки одного цвета, а также 16 квартетов и тройка разных цветов. Или всего имеем 27 наборов разных цветов. Если разместить их по кругу, то первый и последний наборы должны быть разных цветов. То есть красных наборов может быть (27-1):2=13. С каждой стороны красных наборов будут не красные наборы. Таким образом максимум 26 гномов в красных колпаках могут иметь соседа не в красном колпаке.
Задачу можно интерпретировать как 250 опытов с фиксированной вероятностью успеха и неудачи в каждом отдельном испытании, т.е. по факту мы имеем биномиальное распределение, применима формула Бернулли
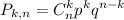
или в нашем случае
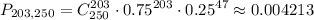
Если мощного калькулятора под рукой нет, то лучше вместо биномиального использовать нормальное распределение. Это допустимо, ведь из центральной предельной теоремы следует что при неограниченном возрастании числа опытов ф-я распределения будет неограниченно приближаться к нормальному распределению (с мат. ожиданием 0 и дисперсией 1)
Формула периметра прямоугольника:
P = 2(а+b), где а — длина, b — ширина.
Формула площади прямоугольника:
S = ab.
Пусть длина прямоугольника равна х, тогда имеем:
P = 2(х+b) = 34
Чтобы найти неизвестный множитель, нужно произведение разделить на известный:
х+b = 34 : 2
х+b = 17
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное:
b = 17 - х — ширина прямоугольника.
Подставим длину и ширину в формулу площади прямоугольника:
S = x(17-x) = 17x - x².
S = 17x - x².