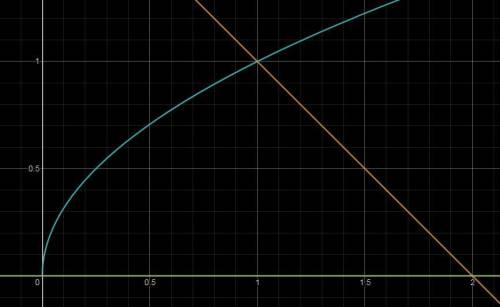
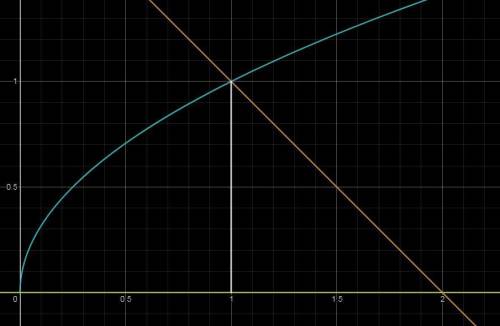
Построим все эти графики в одной системе координат (см. вложение №1). Получившаяся фигура не является криволинейной трапецией, но, проведя прямую 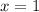 (см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
(см. вложение №2), можно разбить её на две криволинейные трапеции, у каждой из которых можно найти площадь. Искомая площадь является суммой площадей двух составляющих эту фигуру криволинейных трапеций.
Итак, находим площадь левой криволинейной трапеции.
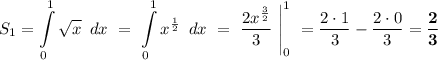
Теперь находим площадь правой криволинейной трапеции.
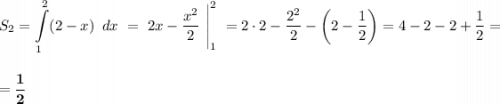
А теперь складываем и находим искомую площадь.
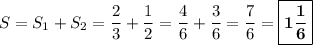 .
.
ответ: 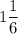 .
.
Каждое значение аргумента х из этого интервала можно представить в виде
x = π/2 + φгде 0 <φ < π/2 . По формулам приведенияsin ( π/2 + φ) = соsφ = sin ( π/2 — φ).Точки оси х с абциссами π/2 + φ и π/2 — φ симметричны друг другу относительно точки оси х с абсциссой π/2, и синусы в этих точках одинаковы. Это позволяет получить график функции у = sin х в интервале [π/2 , π ] путем простого симметричного отображения графика этой функции в интервале [0 , π/2] относительно прямой х = π/2.