Question

Ребята, у меня в садике К/Р была, я не знаю как задачу решить, обьясните... Докажите, что выражение делится на 9 при любом натуральном n:

$2^{2n-1}+3n-5$

Answer 1

${2}^{2n - 1} + 3n - 5$

Шаг 1: база индукции:

n=2 ⇒

${2}^{2 \times 2 - 1} + 3 \times 2 - 5 = 2 ^{3} + 6 - 5 = 9$

Шаг 2: допустим, что утверждение выполняется в случае n=n.

Шаг 3: Если докажем правдивость утверждения в случае n=n+3 то покажем, что наше допущение также правда.

Если разница числа P и Q делится на 9 нацело, то и их разница делится на 9 нацело и наоборот.

P = 9*p

Q = 9*q

P - Q = 9(p-q)

${2}^{2(n + 3) - 1} + 3(n + 3) - 5 = {2}^{2n + 5} + 3n + 4$

Доказательство тому, что n=n

Разница:

$({2}^{2n + 5} + 3n + 4) - ( {2}^{2n - 1} + 3n - 5 = {2}^{2n - 1} (2 {}^{6} - 1) + 9 = {2}^{2n - 1} \times 63 + 9 = 9( {2}^{2n - 1} \times 7 + 1)$

Разница кратна 9, и это доказало кратность выражения в случае n+3, а это подтверждает гипотезу

Answer 2

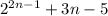
Пошаговое объяснение:

1) Определим значения выражения 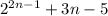$2^{2n-1}+3n-5$ при различных значениях 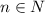$n \in{N}$как последовательность

$a_{n}=2^{2n-1}+3n-5$

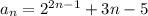
2) Определим значения членов 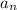$a_n$ последовательности при n=1, n=2, n = 3:

$a_1=2^{2\cdot1-1}+3\cdot1-5 = {2} + 3 - 5 = 0 \\ a_2=2^{2\cdot2-1}+3\cdot2-5 = {2}^{3} + 6 - 5 = 9 \\ a_3=2^{2\cdot3-1}{+}3{\cdot}3{-}5{=}{2}^{5} { +}9 {-} 5 =32{ +} 4{ =}36 \\$

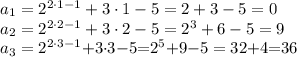
3) Применим метод математической индукции.

3a) Возьмем такой член 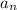$a_n$, который кратен 9 (как мы убедились выше, такое 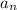$a_n$ существует (например, а3))

Т.к. он кратен 9, обозначим его как

$a_n=9k \:\:\: \:\:\:2^{2n-1}+3n-5=9k$

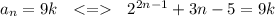
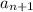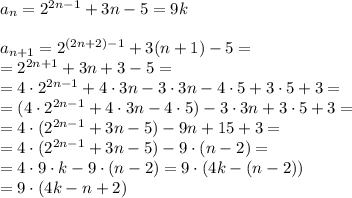
3b) Вычислим значение $a_{n+1}$,

$a_{n} = 2^{2n-1}+3n-5 = 9k \\ \\ a_{n + 1} = 2^{(2n + 2)-1}+3(n + 1)-5 = \\ = 2^{2n + 1}+3n + 3-5 = \\ =4 \cdot2^{2n - 1}+4 \cdot3n - 3 \cdot3n-4 \cdot5 +3 \cdot5 + 3 = \\ =(4 \cdot2^{2n - 1}+4 \cdot3n -4 \cdot5) - 3 \cdot3n+3 \cdot5 + 3 = \\ = 4 \cdot(2^{2n - 1} + 3n - 5) - 9n + 15 + 3 = \\ = 4 \cdot(2^{2n - 1} + 3n - 5) - 9\cdot( n - 2) = \\ = 4 \cdot9\cdot{k} - 9 \cdot(n - 2) = 9 \cdot(4{k} - (n - 2)) \\ = 9 \cdot(4{k} - n + 2)$

Как мы видим, мы получили, что 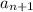$a_{n+1}$ равно произведению, один из множителей которого равен 9, а следовательно, 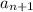$a_{n+1}$ также кратен 9 Следовательно кратность 9 справедлива и для последующих значений последовательности.

Что и требовалось доказать