Question

X²-7x:5+2x=2 хелпаните срч

Answer 1

$x_{1}$ ≈ -1,74568 ; $x_{2}$ ≈ 1,14568

Пошаговое объяснение:

1. Запишим деление в виде дроби

x²-7x:5+2x=2 = x²-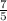$\frac{7}{5}$x+2x=2

2. Вычислим сумму

x²-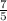$\frac{7}{5}$x+2x=2 = x²+$\frac{3}{5}$x=2

3. Умножаем обе части уравнения на 5

x²+$\frac{3}{5}$x=2 = 5x²+3x=10

4. Переносим константу в левую часть и изменяем её знак

5x²+3x=10 = 5x²+3x-10=0

5. Решаем квадратное уравнение ax²+bx+c=0 используя {

x =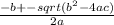 $\frac{-b +- sqrt(b^{2}-4ac)}{2a}$

} :

x =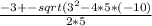 $\frac{-3 +- sqrt(3^{2}-4*5*(-10)}{2*5}$

6. Вычисляем степень

x=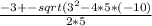$\frac{-3 +- sqrt(3^{2}-4*5*(-10)}{2*5}$ = x=$\frac{-3 +- sqrt(9-4*5*(-10)}{2*5}$

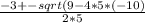
7. Вычисляем произведение

x=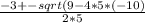$\frac{-3 +- sqrt(9-4*5*(-10)}{2*5}$ = x=$\frac{-3 +- sqrt(9+200)}{10}$

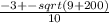
8. Сложим числа

x=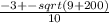$\frac{-3 +- sqrt(9+200)}{10}$ = x=$\frac{-3 +- sqrt(209)}{10}$

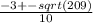
9. Запишим решения: одно со знаком + и одно со знаком -

x=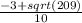$\frac{-3 + sqrt(209)}{10}$

x=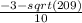$\frac{-3 - sqrt(209)}{10}$

10. Уравнение имеет 2 решения

$x_{1}$=$\frac{-3 + sqrt(209)}{10}$

$x_{2}$=$\frac{-3 - sqrt(209)}{10}$

11. Решение

$x_{1}$=$\frac{-3 + sqrt(209)}{10}$

$x_{2}$=$\frac{-3 - sqrt(209)}{10}$

=

$x_{1}$ ≈ -1,74568

$x_{2}$ ≈ 1,14568

Answer 2

≈ -1,74568 ;  ≈ 1,14568