Найдем сколько столбов установила бригада после i-ого дня.
Пусть после предыдущего (i-1) дня стоит ровно столбов.
Т.к. каждый следующий день столбы устанавливаются строго между уже поставленными, то в i-ый день установят столбов.
Тогда суммарно после i-го дня имеем:
(1)
Теперь, выразим через и подставим в выражение (1).
.
Продолжая выражать члены последовательности через предыдущие, через (i-1) шаг получим:
(2) .
В этом выражении справа видим сумму (i-1) членов геометрической прогрессии c a1=1, q=2. Ее можно также представить в виде:
.
Подставим это в выражение (2):
(3) .
Перепишем получившееся выражение в более удобном виде:
(4) .
Теперь мы видим, что выражение, стоящее слева знака равенства должно быть степенью 2.
По условию в конце работы:
В таком случае, чтобы дробь была степенью 2, знаменатель должен быть вида:
(5) , где k =0,1,2...
Для выполнения условия задачи, необходимо, чтобы в уравнении (4) i было максимально (чтобы работу можно было растянуть на максимальное кол-во дней). Значит нужно минимизировать знаменатель, а это значит выбрать минимальное k в выражении (5), т.е. k=0.
В таком случае:
Подставим это в уравнение (4):
.
Отсюда заключаем, что .
Таким образом, максимальное число дней в которые бригада сможет выполнить работу, сохраняя порядок работы, равно 7.
Памятник А. С. Пушкину был воздвигнут в Москве на Пушкинской площади в 1880 году ко дню рождения поэта. Скульптура Пушкина выглядит очень естественно: правая рука заложена за борт сюртука, левая- непринужденным жестом отведена за спину, она держит шляпу. Немного выдвинутая вперед левая нога создает иллюзию медленного движения, вот-вот поэт сойдет с постамента и спустится к нам. Голова наклонена, его грустные, живые глаза смотрят на нас из глубины веков. Постоянное впечатление, что Пушкин в творческом размышлении: на лбу выступают морщины, на лице видна его полная отвлеченность - думы о чем-то своем. Возможно, это размышления о своей Родине или о трудной судьбе простого русского человека. А возможно, он создает какое-то новое поэтическое произведение. Но весь общий внешний вид - это образ творящего, вдохновенного человека. Его одежда скромна, повседневна, обычна для тех времен. На сюртук накинут длинный плащ, который ниспадает складками. Фигура Пушкина стоит на высоком постаменте, который является символом того, что поэт, его душа, его мысли всегда будут чтить, как нечто возвышенное. Автор памятника Опекушин.
Найдем сколько столбов установила бригада после i-ого дня.
Пусть после предыдущего (i-1) дня стоит ровно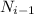
столбов.
Т.к. каждый следующий день столбы устанавливаются строго между уже поставленными, то в i-ый день установят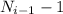
столбов.
Тогда суммарно после i-го дня имеем:
(1)
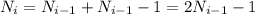
Теперь, выразим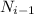
через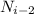 
и подставим в выражение (1).
Продолжая выражать члены последовательности через предыдущие, через (i-1) шаг получим:
(2)
.
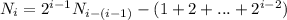В этом выражении справа видим сумму (i-1) членов геометрической прогрессии c a1=1, q=2. Ее можно также представить в виде:
Подставим это в выражение (2):
(3)
.
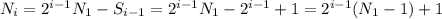Перепишем получившееся выражение в более удобном виде:
(4)
.
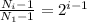Теперь мы видим, что выражение, стоящее слева знака равенства должно быть степенью 2.
По условию в конце работы: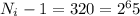
В таком случае, чтобы дробь была степенью 2, знаменатель должен быть вида:
(5)
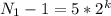, где k =0,1,2...
Для выполнения условия задачи, необходимо, чтобы в уравнении (4) i было максимально (чтобы работу можно было растянуть на максимальное кол-во дней). Значит нужно минимизировать знаменатель, а это значит выбрать минимальное k в выражении (5), т.е. k=0.
В таком случае: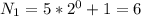
Подставим это в уравнение (4):
Отсюда заключаем, что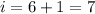
.
Таким образом, максимальное число дней в которые бригада сможет выполнить работу, сохраняя порядок работы, равно 7.