Question

6)Сумма цифр двузначного числа равна 7. Если цифры в этом числе поменять местами, получается число на 27 больше, чем исходное число. Найдите первоначальное число.
3)Если вы увеличите первое число на 7 и уменьшите второе число в 6 раз, сумма этих чисел

составит 29. Если вы уменьшите первое число на 5 и увеличите второе в 2 раза, разница между

вторым и первым числами равно 9. Найдите эти числа.

Answer 1

Задание 6.

Итак, по условию нам дано двузначное число. Двузначные числа - это числа, состоящие из десятков и единиц.

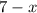Пусть первая цифра - $x$. Тогда вторая цифра = $7-x$ (т.к. по условию их сумма равна 7).

Первое число будет выглядеть как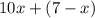 $10x+(7-x)$, т.к. изначально первая цифра стоит в разряде десятков (т.е. умножается на 10), а вторая в разряде единиц (т.е. умножается на 1).

После перестановки же цифры меняются местами, и первая цифра оказывается на втором месте, а вторая - на первом.

Тогда число будет выглядеть так: $10*(7-x)+x$.

Известно, что второе число на 27 больше первого.

Составим и решим уравнение.

$10(7-x)+x-(10x+7-x)=27\\70-10x+x-10x-7+x=27\\63-19x=27\\18x=63-27\\18x=36\\x=2$- первая цифра.

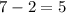Тогда $7-2=5$ - вторая цифра.

Проверка:

$52-25=27$ верно.

Тогда первоначальное число - 25.

ответ: 25.

Задание 3.

Здесь проще всего составить два уравнения, согласно условиям этой задачи.

Пусть первое число - $x$, второе - $y$.

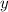"Если вы увеличите первое число на 7" -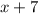 $x+7$, "...и уменьшите второе число в 6 раз" - 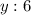$y:6$, "сумма этих чисел составит 29", следовательно,

$x+7+y:6=29$

"Если вы уменьшите первое число на 5" -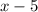 $x-5$, "...и увеличите второе в 2 раза" - 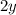$2y$, "разница между вторым и первым числами равна 9",  следовательно, $2y-x+5=9$.

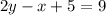Составим систему и решим ее методом подстановки.

$\left \{ {{x+7+y:6=29} \atop {2y-x+5=9}} \right.=\left \{ {{x+y:6=22} \atop {2y-x=4}} \right.=\left \{ {{x+y:6=22} \atop {x=2y-4}} \right.= \left \{ {{2y-4+y:6=22} \atop {x=2y-4}} \right.$  

Теперь решим верхнюю часть отдельно, т.к. мы выразили одну переменную через другую и получили уравнение с одной переменной.

$2y-4+\frac{y}{6}=222y+\frac{y}{6}=26frac{12y+y}{6}=2612y+y=26*6\\13y=156y=\frac{156}{13}y=12$- второе число .

Тогда первое число:

$x=2y-4=2*12-4=20$ - первое число.

Проверка:

$20+7+12:6=29\\27+2=29\\29=29$верно

$12*2-(20-5)=24-15=9$ верно

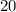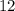ответ: первое число - $20$, второе число - $12$.