Всего 6 рисунков
Пошаговое объяснение:
Число различных рисунков есть то же самое, что и количество различных сочетаний (перестановок) групп по три из трех.
Всего таковых насчитывается 3! (читается как три факториал, а считается как произведение всех натуральных чисел от одного до в данном случае трех)
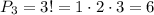
Кратко докажем что это так:
Будем закрашивать в конкретном порядке:
(голова(Г) -> крылья(К) -> хвост(Х))
Г - закрашиваем любыми цветами - их 3
К - закрашиваем любым из оставшихся - их 2
Х - закрашиваем единственным оставшимся - он 1
Отсюда и число сочетаний
Для каждого из 3 разных варианта Г есть по 2 варианта К (мы ведь уже использовали одну краску, т.е. две осталось); итого 3*2=6 вариантов.
И для каждого из 6 вариантов существует по единственному варианту Х (две краски из трех ведь мы использовали)
Итого и получаем 3*2*1 = 1*2*3 = 3! = 6 вариантов рисунков всего
Пошаговое объяснение:Только на перемещение черного коня надо 8 ходов. С белыми я так понимаю, черный конь должен меняться местами, потому что иначе единственный первый ход невозможен - коню с с2 некуда уйти. Если это так, то после прохода черного коня надо еще 6 ходов, чтобы вернуть белых на места. Итого, 14 ходов.
Черного коня доставить меньше, чем за 8 ходов точно нельзя - у него только один путь, без вариантов. Белых может быть можно вернуть на места более оптимальным путем - лениво сейчас считать их варианты, но проще таки возвращать в обратном порядке от того, в котором они ходили.
PS: насчет первого хода я кажется ошибся - можно таки не менять местами коней, а передвигать их по очереди хватает. Но это я точно на ночь глядя не буду - там будет много ходов.