Поясню, в первом действии мы делим обе стороны нашего уравнения на -log(38), получаем 8x+41 = 52-3x, далее перенесём -3х в лево с противоположным знаком. получается 8x+3x=52-41, приводим подобные, в нашем случае это 8x и 3x и произведем вычитание 52 и 41. получим 11х=11, 11:11 = 1 ⇒ х=1
по теореме Пифагора рассчитывай, с2=а2+b2. 2-это квадрат. с-это гипотенуза(та,котороя по горизонтали),а-катет,b-катет(соответствено оставшиеся стороны) 1.Рассмотрим прямоугольный треугольник ABC, где ∠ABC = 90°. Опустим из этого угла высоту h на гипотенузу AC, точку пересечения высоты с гипотенузой обозначим D. 2.Треугольник ADB подобен треугольнику ABC по двум углам: ∠ABC = ∠ADB = 90°, ∠BAD - общий. Из подобия треугольников получаем соотношение сторон: AD/AB = BD/BC = AB/AC. Берем первое и последнее соотношение пропорции и получаем, что AD = AB²/AC. 3.Поскольку треугольник ADB прямоугольный, для него справедлива теорема Пифагора: AB² = AD² + BD². Подставляем в это равенство AD. Получается, что BD² = AB² - (AB²/AC)². Или, что то же, BD² = AB²(AC²-AB²)/AC². Так как треугольник ABC прямоугольный, то AC² - AB² = BC², тогда получим BD² = AB²BC²/AC² или, извлекая корень из обеих частей равенства, BD = AB*BC/AC.4С другой стороны, треугольник BDC также подобен треугольнику ABC по двум углам: ∠ABC = ∠BDC = 90°, ∠DCB - общий. Из подобия этих треугольников получаем соотношение сторон: BD/AB = DC/BC = BC/AC. Из этой пропорции выражаем DC через стороны изначального прямоугольного треугольника. Для этого рассматриваем второе равенство в пропорции и получаем, что DC = BC²/AC.5Из соотношения, полученного в шаге 2, имеем, что AB² = AD*AC. 5.Из шага 4 имеем, что BC² = DC*AC. Тогда BD² = (AB*BC/AC)² = AD*AC*DC*AC/AC² = AD*DC. Таким образом, высота BD равна корню из произведения AD и DC или, как говорят, среднему геометрическому частей, на которые эта высота разбивает гипотенузу треугольника.
" Кактус, так его звали, молча сносил упреки. Он как будто ждал своего часа. " Послушайте!", воскликнула Роза. "Вот уже почти год, как Кактус живет с нами, и еще ни разу он ничем не порадовал ни нас, ни нашу госпожу, которая ухаживает за нами всеми. Какая польза от него?" " Давайте выбросим его на ", предложила фиалка, даже не моргнув синим глазом. " Давайте!", подхватили все. Даже вечнозеленый фикус закричал: " На по-мой-ку!" Кактус заплакал так, как будто сам себя уколол своими колючками в самое сердце. Ему было очень грустно и обидно. Настало следующее утро. Все цветы проснулись, умылись и стали прихорашиваться. Неожиданно они услышали чье-то пение, оно раздавалось из угла подоконника. Как? Что? Почему? Это был... Кактус! Он выглядел просто сказочно! Это была не зеленая толстая колючка, нет, это был грациозный цветок с нежными розовыми лепестками, похожий на звезду, внутри которой живут желтые огоньки. Он так старался произвести впечатление, он так долго к этому шел, что все ахнули! От избытка чувств все зааплодировали и выбрали его Королем. )
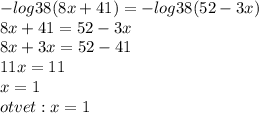
Поясню, в первом действии мы делим обе стороны нашего уравнения на -log(38), получаем 8x+41 = 52-3x, далее перенесём -3х в лево с противоположным знаком. получается 8x+3x=52-41, приводим подобные, в нашем случае это 8x и 3x и произведем вычитание 52 и 41. получим 11х=11, 11:11 = 1 ⇒ х=1