ответ:
1) 67/84 2) 59/216 3) 31/42 4) 907/1430 5) 1219/2100
пошаговое объяснение:
для начала эти дроби к общему знаменателю, в данном случае это 84;
25/28 - 2/21 = 75/84 - 8/84 = 67/84
общий знаменатель для 2-го примера 216;
41/54 - 32/72 = 164/216 - 105/216 = 59/216
общий знаменатель - 42
20/21 - 3/14 = 40/42 - 9/42 = 31/42
общий знаменатель - 1430
40/143 + 39/110 = 400/1430 + 507/1430 = 907/1430
общий знаменатель - 2100
43/140 + 41/150 = 645/2100 + 574/2100 = 1219/2100
Пошаговое объяснение:
В математике есть много подобных «доказательств». В том числе есть и «доказательство» того, что 2*2=5. Но все эти «доказательства» содержат в себе ошибки, но бывает, что их трудно сразу обнаружить. Ученые такими доказательствами не занимаются. Только шутники, которые неплохо знают математику.
То, что 2+2=5 есть много разных «доказательств». Приведу самое Представим равенство: 20-20=25-25. Выносем множители: 4(5-5)=5(5-5) и разделим на общий множитель (5-5). Получим 4=5. Следовательно, 2+2=5. Попробуйте найти здесь ошибку. А всё очень А в математике делить на ноль нельзя.
Ещё одно «доказательство». 2+2=5. Преобразуем это равенство 2 * 1 + 2 * 1 = 5 * 1. Распишем 1 как частное равных чисел: Имем 1 = (5-5)/(5-5). Тогда получим 2 * (5-5)/(5-5) + 2 * (5-5)/(5-5) = 5 * (5-5)/(5-5). Умножим обе части уравнения на(5-5), тогда имеем 2*(5-5) + 2*(5-5) = 5*(5-5) Отсюда получим 0 + 0 = 0. Это доказательство похоже на предыдущее, но лихо закрученное. Здесь также нельзя делить на ноль.
А вот ещё более сложное «доказательство». Докажем что 2+2=5 и 2 * 2 = 5, тоже равно 5. То есть 4=5 . Запишем сначала очевидное равенство 25 - 45 = 16 - 36 . Прибавим (9/2)^2 к обеим частям 25 - 45 + (9/2)^2 = 16 - 36 + (9/2)^2. Или 5^2 - (2 * 5 * 9)/2 + (9/2)^2 = 4^2 - (2 * 4 * 9)/2 + (9/2)^2. Отсюда(5-9/2)^2 = (4-9/2)^2. Обе части положительны, можно извлечь квадратный корень. 5 - 9/2 = 4 - 9/2. Теперь прибавим 9/2 к обеим частям уравнения: 5 = 4 что и требовалось доказать. Итак, 2*2 = 5 и 2+2=5. Где здесь ошибка в доказательстве?
Числитель первой дроби положителен, а вот ее знаменатель отрицателен. Увидеть это можно либо использовав формулу суммы, либо заметив, что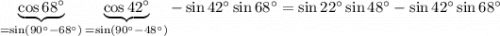
и поскольку синус возрастает на 
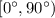, то 
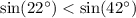и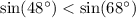 
. Значит, эта дробь отрицательна.
Числитель второй дроби очевидно положителен, как и ее знаменатель: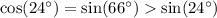
. Значит, эта дробь положительна.