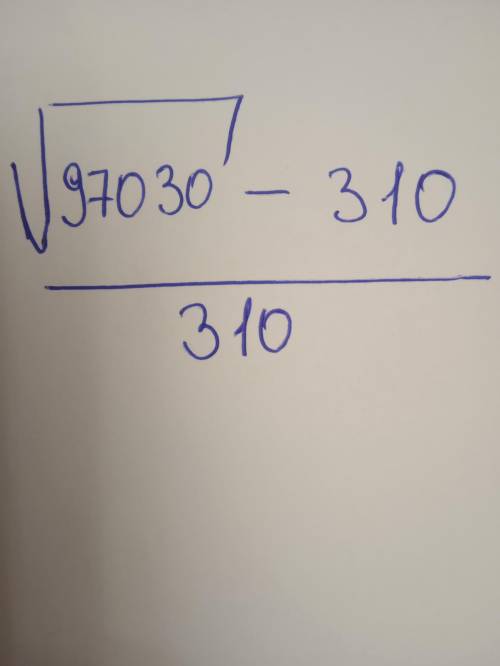
Задание 1
чтобы узнать делиться ли число на 3 нужно чтоб сумма чисел можно было разделить на 3 например
345 это 3 + 4 + 5 = 12 оно кратно 3 то есть делиться на 3.
Дальше мы просто проверяем каждое число .
342, 345, 348, 351 кратны 3 но нам нужны нечётные, поэтому нам подходят 345 и 351
Задание 2
1, 2, 4, 7, 14, 28
Задание 3
а) 48 = 8 * 6 = 2 * 2 * 2 * 2 * 3
б) 60 = 6 * 10 = 2 * 2 * 3 * 5
в) 88 = 4 * 22 = 2 * 2 * 2 * 11
Задание 4
Разложим на простые множители 78
78 = 2 • 3 • 13
Разложим на простые множители 91
91 = 7 • 13
Выберем одинаковые простые множители в обоих числах.
13
Находим произведение одинаковых простых множителей и записываем ответ
НОД (78; 91) = 13 = 13
НОК
НОК (78, 91) = 546
Как найти наименьшее общее кратное для 78 и 91
Разложим на простые множители 78
78 = 2 • 3 • 13
Разложим на простые множители 91
91 = 7 • 13
Выберем в разложении меньшего числа (78) множители, которые не вошли в разложение
2 , 3
Добавим эти множители в разложение бóльшего числа
7 , 13 , 2 , 3
Полученное произведение запишем в ответ.
НОК (78, 91) = 7 • 13 • 2 • 3 = 546
5 задание
а)Разложим на простые множители 78 и 195
78 = 2*3 *13
195 = 3* 5 *13
Одинаковые простые множители в обоих числах - 3 , 13 отсюда получим
НОД (78; 195) = 3 * 13 = 39
б) Разложим на простые множители 80 и 112
80 = 2* 2* 2* 2 *5
112 = 2 *2 *2 *2* 7
В разложении меньшего числа есть множители, которые не вошли в разложение это 5
Добавляем этот множитель в разложение большего числа т.е. 112
2;2; 2; 2 ;7 ;5 и тогда отсюда получим
НОК (80, 112) = 2 *2* 2* 2* 7 * 5 = 560
12 : (4/5х) = 20 : 1/4 5/6 = 15/(2х - 3)
4/5х * 20 = 12 * 1/4 5 : 6 = 15 : (2х - 3)
80/5х = 12 : 4 6 * 15 = 5 * (2х - 3)
16х = 3 90 = 10х - 15
х = 3 : 16 90 + 15 = 10х
х = 3/16 105 = 10х
х = 105 : 10
х = 10,5
(15/2)/(9/2) = х - 3/25
15/2 * 2/9 = х - 3/25
15/9 = х - 3/25
5/3 + 3/25 = х
х = 125/75 + 9/75 = 134/75 = 1 59/75