1) Длина стороны ВС равна √((Xc-Xb)²+(Yc-Yb)²) = √((17-1)²+(2-0)²) =
= √(16²+2²) = √(256+4) = √260 = 2√65 = 16.1245.
Аналогично находим длину стороны АВ = 5, и АС = 13.
2) Площадь S = (1/2)*|(Xb-Xc)*(Yc-Ya)-(Xc-Xa)*(Yb-Ya)| =
= (1/2)*|(1-5)*(2-(-3))-(17-5)*(0-(-3))| = (1/2)*|-4*5-12*3| =(1/2)|-56| = 28.
3) Уравнение стороны ВС:
(X-Xb)/(Xc-Xb) = (Y-Yb)/(Yc-Yb)
(X-1)/(17-1) = (Y-0)/(2-0)
(X-1)/16 = Y/2
X-8Y-1=0 или с коэффициентом: У = (1/8)X - (1/8).
4) Уравнение высоты из вершины А:
(Х-Xa)/(Yc-Yb) = (Y-Ya)/(Xb-Xc)
(X-5)/(2-0) = (Y-(-3))/(1-17)
(X-5)/2 = (Y+3)/-16
8X+Y-37=0 или Y = -8X+37.
Аналогично находим уравнения высоты из вершины В:
12Х+5У-12=0,
и из вершины С:
4Х-3У-62=0.
5) Высота из вершина А равна Ha = 2S/BC = 2*28 / 2√65 = 3,473.
Из вершины В: Нв = 2*28 / 13 = 4,308.
Из вершины С: Нс = 2*28 / 5 = 11,2.
6) Косинус угла В: cosB = (AB²+BC²-AC²) / (2*AB*BC) =
= (5²+(2√65)²-13²) / (2*5*2√65) = 116/20√65 =
0.7194
Угол В = 0.76786 радиан =
43.9949 градуса.
Δ АВС- равнобедренный, 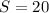 кв. ед.
кв. ед.
Пошаговое объяснение:
Найдем стороны треугольника, воспользовавшись формулой расстояния между точками
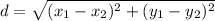

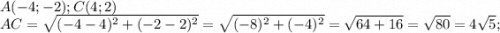
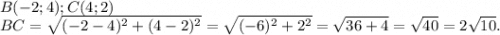
Так как AB=BC , то Δ АВС - равнобедренный.
Проведем высоту ВМ, в равнобедренном треугольнике она является и медианой.
Значит, АМ= МС= 4√5: 2=2√5 ед.
Рассмотрим прямоугольный треугольник Δ АМВ и найдем катет ВМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 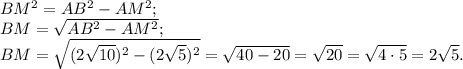
Найдем площадь треугольника как полупроизведение стороны на высоту, проведенную к данной стороне.
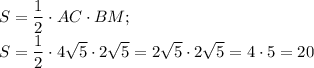

12, 36
6, 12
45, 135