55
Пошаговое объяснение:
1. Если укладывать в ряд по 10 плиток, то для квадратной площадки 10 на 10 плиток не хватает. Значит плиток меньше, чем 100 штук.
2. При укладывании по 8 плиток в неполном ряду может быть от 1 до 7 плиток
3. При укладывании по 9 плиток получается неполный ряд, в котором на 6 плиток меньше, чем при укладывании неполного ряда при 8 плитках. Такое возможно, если есть ряды из 8 плиток и один неполный ряд из 7 плиток.
4. Сколько-то рядов из 8 плиток +7 = Сколько-то рядов из 9 плиток +1.
5. Ищем:
1*8+7=15, но 1*9+1=10
2*8+7=23, но 2*9+1=19
3*8+7=31, но 3*9+1=28
4*8+7=39, но 4*9+1=36
5*8+7=47, но 5*9+1=46 (уже близко!)
6*8+7=55 и 6*9+1=55 (попали).
Количество плиток равно 55.
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от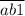 
до 
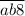, либо от 
до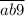 
.
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
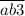, делящееся на 3
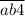, делящееся на 4
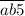, делящееся на 5
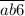, делящееся на 6
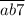, делящееся на 7
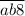, делящееся на 8
Рассмотрим утверждение "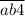 делится на 4". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 
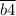делится на 4, 
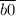делится на 4, 
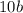делится на 4, 
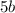делится на 2, значит 
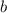- четное.
Рассмотрим утверждение "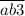 делится на 3". Число делится на 3, если сумма цифр числа делится на 3. Значит, 
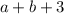делится на 3, 
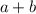делится на 3. Выпишем пары цифр, где 
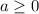, а 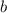- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение "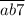 делится на 7". Если 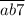делится на 7, то 
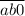делится на 7, 
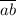делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13
Пошаговое объяснение:
Смотри! Это пропорция. Основное свойство пропорции: произведение крайних членов пропорции ( 4 и 4 ) равно произведению средних членов пропорции ( 8 и 8 ). Пример немного неудачный 4:8=8:4. Если остались вопросы, с удовольствием отвечу!