Вот решение. Сначала надо найти производную функции, затем её приравнять к нулю. Решить уравнение, найти Х. После чертим координатаную прямую на которой и отметим все точки Х. Потом берём числа после и перед точками Х, и подставляем в производную функции. если производная меньше нуля, значит функция на том отрезке убывает, а если больше то возрастает. В данном случае точка экстремумы только одна, и она равна -3,5. Левее неё функция убывает, а правее возрастает. следовательно точка -3,5 - точка минимума функции.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 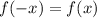 , то функция является чётной.
, то функция является чётной.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 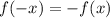 , то данная функция является нечётной.
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда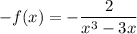 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём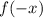 , для этого все
, для этого все  в функции заменим на
в функции заменим на 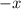 .
.
Таким образом, данная функция является нечётной.
в)
Отсюда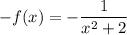 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
То есть, для данной функции за можно принять любое действительное число. Теперь найдём
можно принять любое действительное число. Теперь найдём 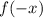 , для этого все
, для этого все  в функции заменим на
в функции заменим на 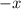 .
.
Таким образом, данная функция является чётной.
г)
Отсюда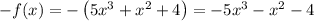 .
.