ВСПОМИНАЕМ 1. Углы при основании равнобедренного треугольника РАВНЫ. 2. Сумма внутренних углов треугольника РАВНА 180 градусам. 3. Развернутый угол РАВЕН 180 градусам.. ДАНО α = 3° - угол между веточками - прямыми. АВ = 1 прыжок ("квак") = CONST - постоянная. НАЙТИ n = ? - число прыжков ("кваков ") для движения ВПЕРЁД. РЕШЕНИЕ Смотрим на рисунок к обратной задаче - найти угол для 8 "кваков" и на доске видим простую формулу - 2 "квака" -> 90/2 = 45°. А теперь решаем нашу задачу с другого конца. ΔABC - равнобедренный -> ∠BCA = α. ∠ABC = 180 - 2*α - сумма углов треугольника ∠ABD - развернутый =180° - отсюда ∠DBC = 180 - 2*α. ∠ACE - развернутый угол И, самое главное, ∠DCE = 180 - α - ∠DBC = 3*α. Смотрим дальнейшие расчеты и видим, что за каждый прыжок угол увеличивается НА α. Движение "вперёд" угол не больше 90°. И тогда формула движения "вперёд". n*α <=90°. Тогда число прыжков n <=90 : α = 90 : 3 = 30 прыжков - ОТВЕТ. Лягушонок промахнулся, но мы решили задачу.
№1.
Как проверить: подставляем координаты в уравнение. Если все совпадает - пара является решением уравнения, если нет - то нет.
(3;1)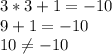
(0;10)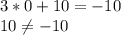
(2;4)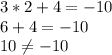
(3;2,5)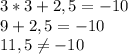
ответ: если дано уравнение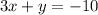 , то ни одна пара не является решением уравнения; если дано уравнение
, то ни одна пара не является решением уравнения; если дано уравнение 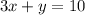 , то подходят пары (3;1), (0;10) (2;4).
, то подходят пары (3;1), (0;10) (2;4).
Примечание: просто я не понял, отрицательное или положительное ли число 10 во второй части данного уравнения, поэтому расписал на оба случая.
№2.
(смотри рисунок)
ответ: (-2;2)
№3.
Метод подстановки:
Выражаем у в первом уравнении:
Подставляем значение у во второе уравнение:
Подставляем значение х в выраженный у, чтобы найти его:
Метод сложения:
Сначала умножим левую и правую части первого уравнения на 7, чтобы можно было сократить у в каждом из уравнений.
Теперь почленно складываем первое и второе уравнения в одно целое:
Подставляем найденный х в любое из уравнений. Я возьму первое уравнение.
ответ: (2;1)