Question

РЕБЯТ , ОЧЕНЬ !!11! Хотя БЫ ОДНО ЗАДАНИЕ 1. Найти НОД и НОК чисел: б) 2 ^37*3^15*12^14 и 3^74*10^28
2.Найдите хотя бы одно рациональное число, расположенное на отрезке [корень из 11; корень из 13 ]
б) Найдите хотя бы одно иррациональное число, расположенное на отрезке [2,1; 2,2]

Answer 1

1. НОД(А,В) = 2²⁸*3²⁹

  НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸

2. а)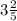 $3\frac{2}{5}$  ; б) $\sqrt{4,6}$

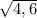
Пошаговое объяснение:

Задание 1.

А= 2³⁷*3¹⁵*12¹⁴ = 2³⁷*3¹⁵*(2²*3)¹⁴ = 2³⁷*3¹⁵*2²⁸*3¹⁴ = 2³⁷⁺²⁸ * 3¹⁵⁺¹⁴ = 2⁶⁵*3²⁹

В = 3⁷⁴ *10²⁸ = 3⁷⁴ *(2*5)²⁸ = 3⁷⁴*2²⁸*5²⁸

НОД(А,В) = 2²⁸*3²⁹

НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸

Задание 2.

a) x∈[√11; √13]  и  x∈Q (Q- множество рациональных чисел)

   x=?

√11 ≈ 3,32       √13 ≈ 3,66

3,32 < x < 3,66

Например, x= 3,4 = 3 4/10 = 3 2/5 (∈Q)

                   x= 3,5 = 3 5/10 = 3 1/2 (∈Q)

                   x= 3,6 = 3 6/10 = 3 3/5 (∈Q)

(приведено сразу 3 примера такого рационального числа, на самом деле, их бесконечное множество).

б) x∈[2,1; 2,2], x∈I (I - множество иррациональных чисел)

  2,1 = √(2,1)² = √4,41

  2,2 = √(2,2)² = √4,84

√4,41 < x < √4,84

Например, х=√4,6 или х=√4,71 или х=√4,782 или х=√4,815

(приведено сразу 4 примера такого иррационального числа, на самом деле, их бесконечное множество).