Question

Чувачки , найти периметр трапеции если ab=cd=10, угол а=60 ad=16

Answer 1

Д. П.:

Проведем BH1 и BH2 - высоты.

1) AB = CD = 10, ⇒

  ABCD - р./б. трапеция (по признаку р./б. трапеции), ⇒

  ∠A = ∠D = 60° (по св-ву р./б. трапеции)

2) Рассмотрим ΔABH1 (∠H1 = 90°)

  ∠ABH1 = 90° - ∠A = 90° - 60° = 30° (по т. о сумме углов в прямоуг. Δ),

  ⇒          

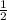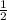  AH1 = $\frac{1}{2}$AB = $\frac{1}{2}$ · 10 = 5 (по теореме)

3) Рассмотрим ΔCDH2 (∠H2 = 90°)

  ∠DCH2 = 90° - ∠D = 90° - 60° = 30° (по т. о сумме углов в прямоуг. Δ),

  ⇒          

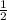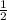  DH2 = $\frac{1}{2}$CD = $\frac{1}{2}$ · 10 = 5 (по теореме)

4) BC = H1H2 = AD - AH1 - AH2 = 16 - 5 - 5 = 6

5) P = AB + BC + CD + AD = 10 + 6 + 10 + 16 =42

ответ: P = 42