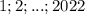
Пошаговое объяснение:
Заметим:
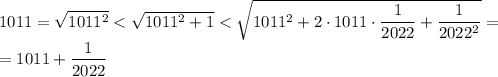
Отсюда

Но это означает, что
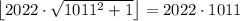
Значит, уравнение равносильно
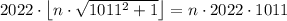
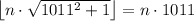
Если решения данного уравнения существуют, то, по определению дробной части числа, верно неравенство
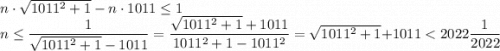
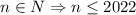
Но для таких значений переменной верны неравенства
![n\cdot 1011< n\cdot\sqrt{1011^2+1}То есть [tex]\forall n\in N, n\leq 2022](/tpl/images/4772/2119/b427d.png) по определению целой части числа равенство
по определению целой части числа равенство 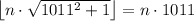 верно. Значит, все натуральные значения
верно. Значит, все натуральные значения 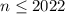 являются корнями данного уравнения.
являются корнями данного уравнения.
![найти все натуральные значения n удовлетворяющие уравнению 2022*[n*sqr(1011^2+1)]=n*[2022*sqr(1011^2](/tpl/images/4772/2119/4fbf9.jpg)
Пошаговое объяснение:
![A= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\a_{31}&a_{32}&a_{33}\end{array}\right] .\\](/tpl/images/1339/9063/2adb9.png)
Так как в данной задаче сумма каждого столбца
должна быть равна 1, ⇒

Матрица приобретает вид:
![A= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &\frac{1}{3} \end{array}\right] .\\](/tpl/images/1339/9063/50d90.png)
Найдём собственный вектор х'', отвечающий
собственному значению λ=1.
Для этого решим уравнение: (А-Е)*х''=0''.
Найдём А-Е:
![A-E= \left[\begin{array}{ccc}\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &\frac{1}{3} \end{array}\right] -\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]= A= \left[\begin{array}{ccc}-\frac{1}{2} &\frac{1}{4} &\frac{1}{3} \\\frac{1}{3} &-\frac{1}{2} &\frac{1}{3} \\\frac{1}{6} &\frac{1}{4} &-\frac{2}{3} \end{array}\right] .\\](/tpl/images/1339/9063/1f878.png)
Тогда еравнение (А-Е)*х''=0'' можно записать в виде следующей однородной системы линейных алгебраических
уравнений:
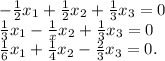
Выполним преобразования.
Умножим первое уравнение на -6, второе уравнение на 3,
а третье уравненик на 12:
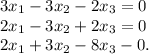
Решим эту систему методом Гаусса.
Запишем расширенную матрицу системы:
![\left[\begin{array}{ccc}3&-3&-2|0\\2&-3&2}|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/9c0f4.png)
Разделим вторую строку на 2:
![\left[\begin{array}{ccc}3&-3&-2|0\\1&-1,5&1|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/9bbf4.png)
Поменяем местами первую и вторую строки:
![\left[\begin{array}{ccc}1&-1,5&1|0\\3&-3&-2|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/de34e.png)
Прибавим ко второй строке первую, умноженную на -3:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\2&3&-8|0\end{array}\right].](/tpl/images/1339/9063/3f887.png)
Прибавим к третьей строке первую, умноженную на -2:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\0&6&-10|0\end{array}\right].](/tpl/images/1339/9063/c8ad4.png)
Прибавим к третьей строке вторую, умноженную на 4:
![\left[\begin{array}{ccc}1&-1,5&1|0\\0&1,5&-5|0\\0&0&-30|0\end{array}\right].](/tpl/images/1339/9063/683c4.png)
Таким образом:
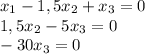
Разделим третью строку на -30:
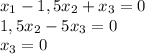
Следовательно:
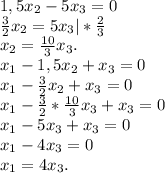
Пусть х₃=с ⇒
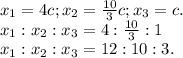
ответ: x₁:x₂:x₃=12:10:3.
Пошаговое объяснение:
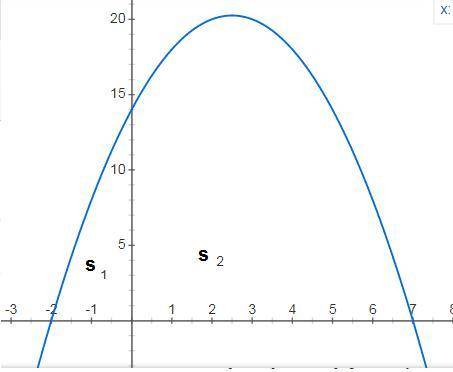
найдем точки пересечения с ОХ
5x+14-x²=0; умножим на -1 ; x²-5x-14=0 ; x₁₋₂=(5±√(25+56)/2=(5±√81)/2=
=(5±9)/2={-2;7}
найдем отдельно площади для х≤0 х≥0 и сложим
₀ ₀
S₁=-∫(5x+14-x^2)dx=-[(5x²/2)+14x-(x³/3)]=-[(5*4/2)-14*2+8/3]=
⁻² ⁻²
=-[10-28+(8/3)]=18-2 2/3=16-2/3=15 1/3
₇ ₇
S₁=∫(5x+14-x^2)dx=[(5x²/2)+14x-(x³/3)]=
⁰ ⁰
=-[(5*49/2)+14*7-342/3]=122,5+98-114=106,5=106 1/2
S=S₁+S₂=15 1/3+106 1/2=121 5/6 кв. единиц
Пусть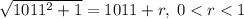 . Заметим, что
. Заметим, что 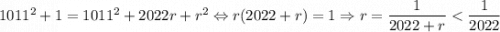 , поэтому
, поэтому ![\left[2022\cdot \sqrt{1011^2+1}\right] = \left[2022\cdot 1011+2022r\right] = 2022\cdot 1011](/tpl/images/4772/2119/bb2c0.png) . Тем самым уравнение перепишется в виде
. Тем самым уравнение перепишется в виде ![2022\cdot \left[n\cdot\sqrt{1011^2+1}\right] = 2022\cdot 1011\cdot n \Leftrightarrow \left[n\cdot\sqrt{1011^2+1}\right] = 1011\cdot n](/tpl/images/4772/2119/17a2f.png) .
.
Теперь подход примерно такой же:![\left[1011n+nr\right] = 1011 n](/tpl/images/4772/2119/78107.png) . Если
. Если 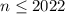 , то равенство выполняется. Пусть
, то равенство выполняется. Пусть 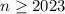 . Тогда
. Тогда 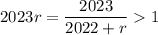 , значит, равенство выполняться уже не будет. Получаем, что решениями будут натуральные числа
, значит, равенство выполняться уже не будет. Получаем, что решениями будут натуральные числа 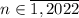 .
.