Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
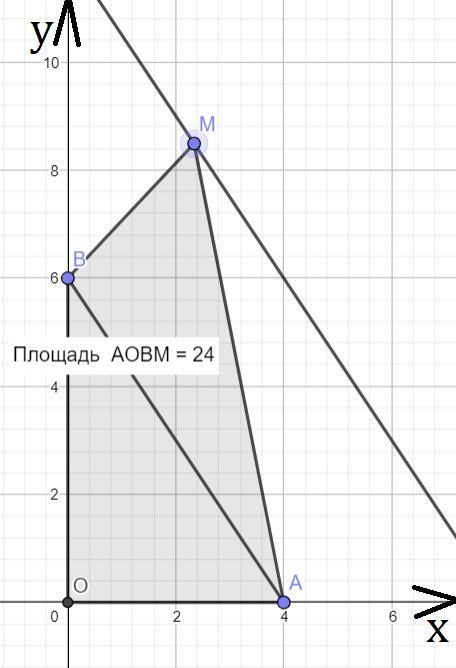
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
чтобы найти промежутки монотонности , надо найти производную функции
прроизводная этой функции равна у=10х+10
теперь найдем нули функции 10х=-10
х=-1
критическая точка равна -1
теперь строим числовую прямую на ней отмечаем критическую точку -1.
теперь возьмем дежурную точку 0 и подставим в функцию где 0, нам отрицательно, т.е. функция убывает
где положительно там возратстает
т.е. - бесконечности до -1 функция возрастате, -1, до плюс бесконечности функция убывает , точка -1 - точка максимума
x = 0
Пошаговое объяснение:
По правилу раскрытия модуля
x >= 0, то модуль x = x
x < 0, то модуль x = -x
В первом случае x <= 0
Во втором случае:
-x <= 0
x >= 0
Объединяя решения данных неравенств, получаем, что x = 0