Формула связи скорости, времени и расстояния:
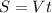
где S - расстояние, V - скорость, а t - время.
Если два грачонка вылетели навстречу друг другу, значит, потратили одинаковое время на путь друг до друга.
Пусть расстояние, пройденное Гошей до встречи, обозначается как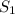 
. Тогда расстояние, пройденное Пашей до встречи, обозначается как 
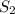, а их скорости обозначим за 
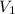и 
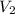соответственно. Общее расстояние равно сумме пройденных двумя грачатами расстояний до встречи: 
.
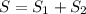Тогда при равенстве затраченного времени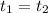 
справедливо равенство:
Отсюда:
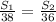
Значит, 
Введя коэффициент пропорциональности 
, получим, что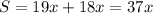 
А вот дальше при текущих условиях эту задачу не решить. Нужно или знать разницу между расстояниями, или хотя бы одно из расстояний, чего нет в условии.
Обозначим положительные корни второго уравнения как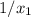 
и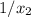 
. Так как сами корни положительны, то и 
, 
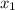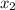тоже положительны и не равны.
Подставим эти корни во второе уравнение, получатся уравнения вида
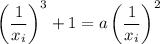
Умножим это уравнение на положительное число вида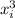 
, получим первое уравнение:
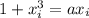
Поскольку 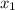и 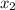- положительные неравные числа, то они и являются корнями первого уравнения. По условию, отношение большего к меньшему равно 2018, пусть для определённости 
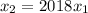. Тогда отношение корней второго уравнения равно
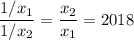
P.S. на самом деле, из условия можно определить значение a. Оно оказывается равным
![\dfrac{4074343}{\sqrt[3]{4074342^2}}](/tpl/images/0958/4050/8a9fc.png)
