Question

Усі ребра правильної трикутної прямої призми рівні. Знайдіть висоту основи призми, якщо об’єм фігури дорівнює 18 см3.

Answer 1

Высота основания призмы равна 3 см.

Объяснение:

Найти высоту основания правильной треугольной призмы, все ребра которой равны между собой, а ее объем равен 18 см³.

Дано: правильная треугольная прямая призма, все ребра равны, V = 18 см³.

Найти: высоту основания.

Решение.

Рисунок прилагается.

Призма называется прямой, если ее боковые ребра перпендикулярны плоскости основания.Прямая призма называется правильной, если в ее основании лежит правильный многоугольник.Объем призмы равен произведению площади основания на высоту:
V = Sосн · H.

1) Выразим объем призмы.
Обозначим ребро призмы a см.
Так как по по условию призма прямая и правильная, то
- в основании призмы лежит равносторонний треугольник,
- боковое ребро ее перпендикулярно основанию и равно высоте призмы.

Сторона треугольника основания равна a см.

Высота призмы также равна длине ребра и равна a см.

Тогда объем нашей призмы:
V = S осн · H =  S осн · a.

Площадь треугольника равна половине произведения двух сторон треугольника на синус угла между ними.
$\displaystyle S_{\Delta} = \frac {1}{2}a \cdot b \cdot \sin \alpha.$

2) Выразим площадь треугольника - основания призмы, через сторону (a см).

У нас треугольник равносторонний, то есть все его стороны равны a см, все углы равны по 60°.

$\displaystyle S_{\Delta} = \frac {1}{2}a^{2} \cdot \sin60^{o} = \frac {1}{2}a^{2} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{4} \cdot a^{2}.$

3) Зная объем призмы и выражения площади основания, найдем длину ребра.

$\displaystyle V = S_{\Delta} \cdot H = \frac{\sqrt{3}}{4} \cdot a^{2} \cdot a = \frac{\sqrt{3}}{4} \cdot a^{3} \\\\ \frac{\sqrt{3}}{4} \cdot a^{3} = 18;\\\\a^{3} = \frac{18 \cdot 4}{\sqrt{3}} =\frac{18 \cdot 4\cdot \sqrt{3}}{3} = 24 \cdot \sqrt {3}.$

Откуда:

$\displaystyle a^{3}= 24 \cdot \sqrt {3}=8 \cdot3\cdot 3^{\frac{1}{2} }=2^{3}\cdot3^{\frac{3}{2} } = (2\sqrt{3})^{3};\\\\a = 2\sqrt{3}\;(cm).$

4) Найдем площадь основания, зная сторону равностороннего треугольника.

$\displaystyle S_{\Delta} = \frac{\sqrt{3}}{4} \cdot a^{2} = \frac{\sqrt{3}}{4} (2\sqrt{3})^{2} = \frac{\sqrt{3} \cdot 4 \cdot 3}{4} =3 \sqrt{3} \;(cm^{2}).$

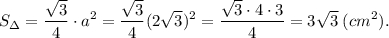
Площадь треугольника равна половине произведения основания на высоту.
$\displaystyle S_{\Delta} = \frac{1}{2} ah.$

5) Найдем высоту основания призмы, то есть высоту h треугольника.

$\displaystyle S_{\Delta}=\frac{1}{2} ah = 3\sqrt{3};\\\\\frac{2\sqrt{3} \cdot h}{2} =3\sqrt{3};\\\\\sqrt{3} \cdot h = 3\sqrt{3};\\\\h = 3\;(cm).$

Таким образом, высота основания призмы равна 3 см.