s1=0, s2=3, s3=-3
Пошаговое объяснение:
Нaверное иммется в виду
(s^3-9s)/10=0, где ^ -означает возведение в степень.
Умножим все на 10
s^3-9s=0
то же, что
s*(s^2-9)=0
Произведение равно 0, если любой из сомножителей равен 0.
Значит один корень s1=0
Два других корни уравнения s^2-9=0
s2=3, s3=-3
25
Пошаговое объяснение:
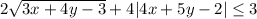
Так как x и y целые, выражение 4x+5y-2 тоже целое. Если оно не равно 0, то его модуль хотя бы 1, второе слагаемое в левой части неравенства хотя бы 4, а первое неотрицательно, то есть неравенство не выполняется.
Значит, 4x+5y-2=0, и неравенство принимает вид
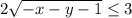
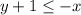
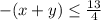
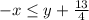
Значит, x может быть равен -y-1 и -y-3.
Если x=-y-c, то, подставив это равенство в выражение, равное нулю, получим
-4y-4c+5y-2=0
y=4c+2, x=3c+2, x+y=7c+4. Максимальная сумма у нас будет при c=3. Она равна 25.
P.S. откуда задачка? не в первый раз сегодня вижу подобные
Пошаговое объяснение:
такое, если да, то щас решу