1) 18-12=6 - разница
2) 30:6=5 (ведер) - за 1 мин каждый насос
3) 12×5=60 (ведер) - первый насос
4) 18×5=90 (ведер) - второй насос
ответ: первый насос - 60 ведер, второй насос - 90 ведер.
Пошаговое объяснение:
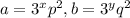, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
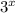, получим уравнение 
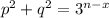. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 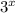, имеем 
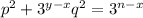. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
60 и 90
Пошаговое объяснение:
второй насос накачал 30 вёдер за 6 мин
30/6=5 - вёдер за 1 мин
5*12=60 - 1 насос
5*18=90 - 2 насос