Question

Начинающий датасайнист написал классификатор писем для электронной почты. Алгоритм помещает нежелательную рекламу в папку “Спам” в 96% случаев и ошибочно отправляет в “Спам” 1% всех обычных писем. Известно, что 10% всех входящих писем — реклама. Вычислите вероятность того, что письмо на самом деле является спамом, когда классификатор отметил его так.

Answer 1

Вероятность того, что письмо на самом деле является спамом, когда классификатор отметил его так равна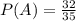 $\displatstyle P(A)=\frac{32}{35}$ .

Пошаговое объяснение:

                                      Процент от всех писем     Попадают в Спам

Обычные письма                                                                     1 %

Нежелательная реклама          10 %                                   96 %

Требуется найти вероятность того, что письмо на самом деле является спамом, когда классификатор отметил его так.

Пусть всего на почту приходит х писем. Из условия 10 % из них реклама, тогда 100 % - 10 % = 90 % - обычные письма.

Отсюда 0,1х  писем - реклама, 0,9х писем - обычные письма.

Исходя из этого

0,96 · 0,1х = 0,096х - это нежелательная реклама, которая попадает в папку Спам.

0,01 · 0,9х = 0,09х - это обычные письма, ошибочно отправленные в Спам.

Количество всех писем попадающих в папку Спам, можно вычислить как сумму

0,096х + 0,009х = 0,105х

Вероятность — это степень возможности, что какое-то событие произойдет. Вероятность вычисляется по формуле

P(A) = m/n

где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Пусть А - событие, при котором классификатор отметил письмо Спамом и оно действительно является таковым.

Тогда n - это число всех писем попадающих в папку Спам, а m - количество писем в папке Спам, которые являются рекламой.

Выполним вычисления:

$\displatstyle P(A)=\frac{m}{n}=\frac{0,096x}{0,105x} =\frac{96}{105} =\frac{32}{35}$

То есть вероятность того, что письмо на самом деле является спамом, когда классификатор отметил его так равна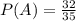 $\displatstyle P(A)=\frac{32}{35}$.