Количество сочетаний из 6 по 2.
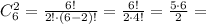
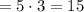 .
.
1) Вероятность промахнуться из пристрелянного пистолета равна 1 — 0,8 = 0,2.
Вероятность взять пристрелянный пистолет равна 0,3 (3 из 10).
Вероятность взять пристрелянный пистолет и при этом промахнуться равна 0,2 · 0,3 = 0,06
2) Вероятность промахнуться из непристрелянного пистолета равна 1 — 0,3 = 0,7.
Вероятность взять непристрелянный пистолет равна 0,7 (7 из 10).
Вероятность взять непристрелянный пистолет и при этом промахнуться равна 0,7 · 0,7 = 0,49
3) Вероятность 1 события или 2 события равна 0,06 + 0,49 = 0,55.
ответ: 0,55
Задача по теории вероятностей. Из 13 лотерейных билетов 5 – выигрышных. Первый студент вынимает наудачу 3 билета (без возвращения), после чего второй студент берет 2 билета. Один из билетов второго студента оказался выигрышным. Какова вероятность того, что у первого студента один из трех билетов выигрышный?
Решение: По условию задачи второй студент взял два билета и один оказался выигрышным.Осталось 11 билетов из которых 4 выигрышных.
Применяем формулу классической вероятности и находим вероятность того, что у первого студента один билет из трех будет выигрышным:
где -число взять один билет выигрышный и два невыигрышных,
- число всех взять 3 из 11 билетов.
Из урны, содержащей 5 красных, 3 черных и 2 белых шара, наудачу извлекают 3 шара. Найти вероятности событий:
А – “все извлеченные шары красные”;
В – “ все извлеченные шары – одного цвета”;
С – “среди извлеченных ровно 2 черных”.
Элементарным исходом данного СЭ является тройка (неупорядоченная !) шаров. Поэтому, общее число исходов есть число сочетаний: n == 120 (10 = 5 + 3 + 2).
Событие А состоит только из тех троек, которые извлекались из пяти красных шаров, т.е. n(A)== 10.
Событию В кроме 10 красных троек благоприятствуют еще и черные тройки, число которых равно= 1. Поэтому: n(B)=10+1=11.
Событию С благоприятствуют те тройки шаров, которые содержат 2 черных и один не черный. Каждый выбора двух черных шаров может комбинироваться с выбором одного не черного (из семи). Поэтому: n(C) = = 3 * 7 = 21.
Итак: Р(А) = 10/120; Р(В) = 11/120; Р(С) = 21/120
Вот тебе выбирай вроде так
Пошаговое объяснение: