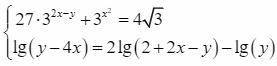
ответ - "силой Разума"
Если функция задана в виде полинома, например, в виде
a*x⁵ + b*x⁴ + c*x³ + d*x² + e*x + f = 0, то :
функция будет нечётной, если в ней только нечётные степени при Х и Y(-x) = - Y(x) - нечётная функция.
функция будет чётной, если в ней только чётные степени при Х и
Y(-x) = Y(x) - чётная функция.
Пошаговое объяснение:
а) f(x) = x² - 4*x² = - 3*x² - степени только чётные - функция чётная.
Проверяем
f(-x) = - 3*(-x)² = - 3*x² = f(x) - чётная - ОТВЕТ
б)
f(x) = x - 5 = x¹ - 5*x⁰ - степени при Х и нечётные и чётные - так и функция - ни чётная ни нечётная - ОТВЕТ
Проверяем на цифрах.
f(-x) = -x - 5 = - (x + 5) ≠ - f(x) ≠ f(x)
Приведем пример, как найти производную второго порядка от функции x*sin(x):
В вышеуказанном калькуляторе вводим x*sin(x) - этим самым мы вычисляем производную первого порядка (должно получиться x*cos(x) + sin(x), копируем найденное )
Теперь выполняем аналогичные операции в калькуляторе, но с найденной первой производной, а именно вводим функцию (вставляем из копированного) x*cos(x) + sin(x)
Получаем ответ (но это только наш пример!): 2*cos(x) - x*sin(x)
Чтобы найти производную третьего порядка (тоже самое что и третья производная функции), то надо проделать первые два пункта выше, в третьем же пункте опять подставить в калькулятор.
Для нашего примера, надо подставить 2*cos(x) - x*sin(x) и получим ответ для третьей производной (опять же это наш пример): -3.0*sin(x) - x*cos(x)
Пошаговое объяснение:Прочитать внимательно
4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))
Пошаговое объяснение:
ОДЗ проверим получив решения.
Второе уравнение при выполнении ОДЗ
равносильно
у-4х=(2+2х-у)^2/y
y^2-4ху=(2+2х-у)^2
y^2-4ху=4+y^2+4x^2+8x-4y-4xy
0=4+4x^2+8x-4y
y=(x+1)^2
2x-y=2x-x^2-2x-1=-x^2-1
3^(2x-y)=(1/3) 3^(-x^2)
Обозначим 3^(х^2)=a
9/a+a=4*sqrt(3)
a^2-4*sqrt(3)*a+9=0
По теореме Виета а1=3*sqrt(3) а2=sqrt(3)
Значит х^2=1,5 или х^2=0,5
Пусть х=sqrt(1,5)
тогда у1=(1+sqrt(1,5)):2=2,5+2*sqrt(1,5)
По ОДЗ подходит 2,5-2*sqrt(1,5)>0
Если х=-sqrt(1,5), то
у=(1-sqrt(1,5))^2=2,5-2*sqrt(1,5) убеждаемся, что по ОДЗ подходит.
Пусть х=sqrt(0,5)
y=1,5+2*sqrt(0,5) по ОДЗ подходит
Пусть х=-sqrt(0,5)
у=1,5-2*sqrt(0,5) по ОДЗ подходит
Итак, 4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))