Пошаговое объяснение:
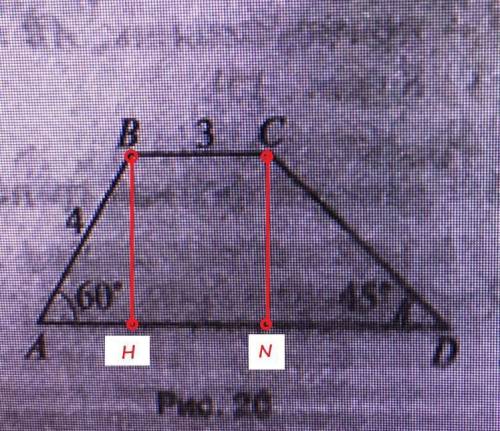
Проведем высоту ВН. Получим треугольник АВН, у которого угол АВН=30*. Тогда АН=1/2АВ=4*1/2=2.
Найдем высоту ВН.
ВН^2=FD^2-AH^2=4^2-2^2=16-4=12;
BH=√12=2√3.
Проведем высоту CN. Получим треугольник CDN, у которого угол CDN равен углу NCD и равен 45*. Следовательно треугольник CDN - равнобедренный и CN=DN. Но CN=BH=√12. Следовательно DN=CN=BH=√12=2√3.
Основание AD=AH+HN+ND=2+3+√12=5+√12.
Найдем сторону CD. CD^2=CN^2+DN^2=(√12)^2+(√12)^2=12+12=24;
CD=√24=2√6.
Периметр P(ABCD)=AB+BC+СD+AD=4+3+2√6+5+√12=2√3+2√6+12.
Площадь S(ABCD)=BH*(AD+BC)/2=2√3(5+2√3+3)/2=8√3+6.
См. скриншот.
1. х = -7
2. х = ±1 7/15
Пошаговое объяснение:
1. х - (-92) = 85 х + 92 = 85 х = 85 - 92 х = -7
Проверка: -7 -(-92) = -7 + 92 = 85 - верно
2. |х|- 0,8= 2/3 |х| = 2/3 + 0,8 |х| = 2/3 + 4/5
|х| = 10/15 + 12/15 |х| = 22/15 = 1 7/15 х = ±1 7/15
Проверка:
при х = 1 7/15 = 22/15
|22/15|- 0,8 = 22/15 - 4/5 = 22/15 - 12/15 = 10/15 = 2/3 - верно
при х = -1 7/15 = -22/15
|-22/15| - 0,8 = 22/15 - 4/5 = 22/15 - 12/15 = 10/15 = 2/3 - верно