Итак, для ограничения по целым степеням не более 27 по модулю, вычислимыми оказались результаты ~957 млн выводов и среди них 356 являются выводами числа 5479 и ни один вывод (а соответственно ни один вывод с операциями сложения, вычитания, конкатенации, умножения и деления, а также некоторые выводы с этими же операциями и некоторыми целыми степенями) не является выводом числа 10958. В чем его особенность?
Призраки и тени
Для задачи, аналогичной задаче Танежи в восходящем порядке, но с начальными векторами длины 8, такими как $(1, 2, ... , 8)$ и $(2, 3, ... , 9)$ количество вариантов меньше, а с иррациональными, комплексными и длинными целыми значениями элементов векторов (1) — (7) справляются оптимизированные алгоритмы Вольфрам Математики. Так, достоверно известно, что ни один вывод в $(1, 2, ... , 9)$, имеющий на 8-ой итерации оператор конкатенации, сложения или вычитания не может привести к значению 10958. Какие возможности для дальнейшего решения это даёт?
Число 10958 является полупростым. И если последняя итерация вывода не содержит сложение, вычитание и конкатенацию, то один из операндов на 8-ой итерации будет гарантировано включать 5479 в некоторой степени, за исключением двух случаев:
когда операнды кратны некоторым комплексно-сопряжённым
когда один из операндов содержит логарифм, основание или показатель которого кратны 5479
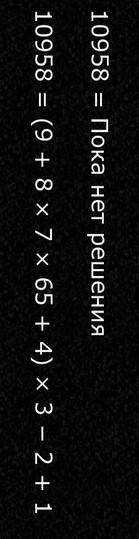
Целое число делится на 3,если сумма его цифр делится на 3,если же сумма цифр данного числа не делится на 3,то и само число не делится на 3.
Число делится на 5,только если на конце этого числа (0 или 5).
Число делится на 6,если сумма его цифр делится на 3.
Число делится на 7,если результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например:259=25-(2*9)=7 делится на 7).
Число делится на 10,только если на конце стоит ноль.
Число делится на 4,если две последние цифры числа делятся на 4 (Например 1120-последние две цифры 20,которые делятся на 4,значит и все число делится).
200-(15+15)×2=140.И это ответ.