тугулымского района, после окончания свердловского сельскохозяйственного института факультета механизации, в качестве инженера-механика. в 1976 году на районной комсомольской конференции был избран вторым секретарем рк влксм. в 1978 году перешел работать начальником инспекции госсельтехнадзор. в 1986 году по решению рк кпсс был рекомендован главным инженером в совхоз «журавлевский. в 1990 году организовал свое крестьянское хозяйство, а в последствии был избран председателем ассоциации крестьянских (фермерских) хозяйств.
педагогическая деятельность началась с 1982 года в качестве руководителя
технического кружка при цдт по совместительству, а с 1992 года был принят штатным педагогом дополнительного образования. защитился на 2 категорию при свердловском дворце молодежи как педагог дополнительного образования. с ноября 1999 года работаю в тугулымской школе в качестве преподавателя-организатора обж. в 2000 году аттестован на 2 категорию. с сентября 2000 года по август 2003 года был назначен директором этой же школы. как руководитель образовательного учреждения аттестован на 1 категорию в 2001 году в г. камышлове. в декабре 2006 года аттестовался на 1 категорию как преподаватель - организатор обж. принимаю активное участие в работе методических объединений, семинаров, в проведении годичных совещаний.
ответ:
Пошаговое объяснение:
Пусть:
Тогда уравнение принимает вид:
Заметим, что если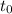
корень уравнения 
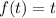, то он и корень уравнения:
Найдем все такие корни:
Заметим, что функция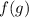
- монотонно возрастает.
Предположим, что в уравнении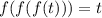
существует корень 
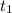, такой, что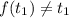 
Рассмотрим случай: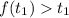
.
Поскольку,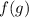
- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 
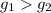, то верно и данное неравенство: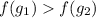 
Из данного утверждения следует, что :
Но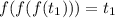
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая