Пошаговое объяснение:
так как один из корней равен 0 их произведения равно 0.
x^4+16-x^2+4x-16=0
x^4-x^2+4x=0
x(x^3-x+4)=0
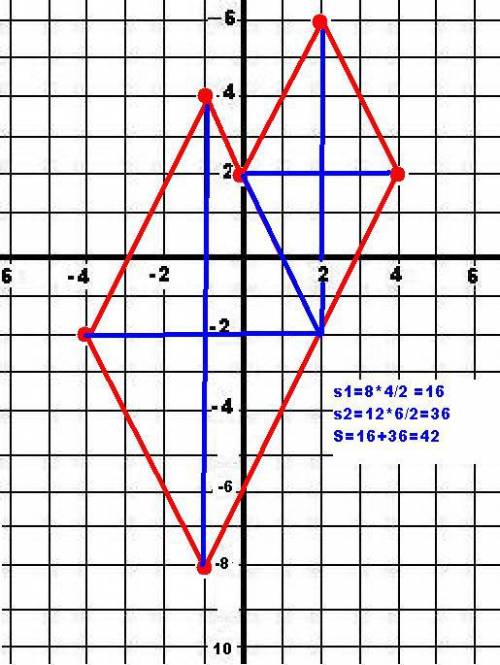
Для начала нужно построить координатную плоскость ху.
Вершины имеют определенные координаты, которые надо отметить на построенной плоскости (я брала 1 клетку за 1 см).
По рисунку видно, что полученная фигура похожа на 2 ромба.
Для того, чтобы посчитать площадь этой фигуры мы используем формулу площади ромба S = 1/2 d1d2, где d1 и d2 – диагонали ромба.
Эти диагонали мы можем узнать из получившегося рисунка (просто измерить линейкой расстояние).
Отметим точку L.
Рассмотрим ромб BAFL.
BF=12см, LA=6см.
Следовательно S BAFL = 1/2*(12*6) = 36см.
Аналогично с ромбом CLED
LD=8 см, CE= 4 см.
S CLED= 1/2*(8*4) = 16 см.
Воспользуемся формулой для корней квадратного уравнения, чтобы найти решения.
−
b
±
√
b
2
−
4
(
a
c
)
2
a
Подставляем значения
a
=
1
,
b
=
4
и
c
=
−
16
в формулу корней квадратного уравнения и решаем относительно
x
.
−
4
±
√
4
2
−
4
⋅
(
1
⋅
−
16
)
2
⋅
1
Упростим.
Нажмите, чтобы увидеть больше шагов...
x
=
−
2
±
2
√
5
Результат можно выразить в различном виде.
Точная форма:
x
=
−
2
±
2
√
5
Десятичный вид:
x
=
2,47213595
…
;
−
6,47213595
…
Пошаговое объяснение: