Пошаговое объяснение:
2,5 часа поездки скорость — 90 км/ч.
1 час поездки скорость — 29 км/ч.
30 минут поездки скорость — 20 км/ч.
Найдите среднюю скорость автомобиля на протяжении всего пути.
30 минут = 0,5 часа
Средняя скорость – это отношение пути ко времени прохождения этого пути. Скорость движения при этом не обязана быть постоянной.
S = V * t, где S - путь (км); V - скорость (км/ч); t - время (ч).
Vср. = (S1 + S2 + S3) / (t1 + t2 + t3)
S1 = 90 * 2,5 = 225 км
S2 = 29 * 1 = 29 км
S3 = 20 * 0,5 = 10 км
Vср. = (225 + 29 + 10) / (2,5 + 1 + 0,5) = 264 / 4 = 66 км/ч
ответ: средняя скорость автомобиля на протяжении всего пути составила 66 км/ч.
2Cos2x – Cos x - 1 = 0
Представим Cos2x = cos²x - sin²x
Из основного тригонометрического тождества cos²x + sin²x = 1 выразим sin²x
sin²x = 1 - cos²x
Получается cos²x - sin²x = cos²x - ( 1 - cos²x) = cos²x - 1 + cos²x = 2 cos²x - 1
Подставляем в изначальное уравнение
2*(2 cos²x - 1) – Cos x - 1 = 0
4 cos²x - 2 – Cos x - 1 = 0
4 cos²x – Cos x - 3 = 0
Пусть cos x = t , тогда
4t² - t - 3 = 0
D = (-1)² - 4 * 4 * (-3) = 1 + 48 = 49 = 7²
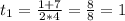
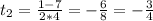
Вернёмся к замене:
cos x = 1
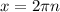 , n∈Z
, n∈Z
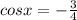
x = ± arccos 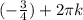 , k∈Z
, k∈Z
ответ: 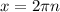 , n∈Z ; x = ± arccos
, n∈Z ; x = ± arccos 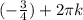 , k∈Z .
, k∈Z .