
Дана функция y=x³ +12x²+45x+50.
1. Определить область определения функции:
ограничений нет, вся числовая ось: D(f) = R.
2. Исследовать функцию на четность не четность:
f(-x) = (-x)³ + 12(-x)² + 45(-x) + 50 = -x³ + 12x²- 45x + 50 ≠ f(x),
f(-x) = -(x³ - 12x²+ 45x - 50) ≠ f(x). Значит, функция общего вида.
3. Найти координаты точек пересечения графика функции с осями координат:
- с осью Оу при х = 0. у = 50.
- с осью Ох при у = 0.
Надо решить уравнение x³ + 12x²+ 45x + 50 = 0.
Находим корни этого уравнения среди множителей свободного члена.
50 = +-1*+-2*+-5*+-5.
При подстановке определяем: х = -2 и х = -5 (2 раза).
x³ + 12x²+ 45x + 50 = (х + 2)*(х + 5)*(х + 5) = 0. х = -2 и х = -5.
4. Исследовать функцию на непрерывность, определить характер точек разрыва функции, если они имеются; найти асимптоты кривой:
точек разрыва и асимптот функция не имеет.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
Производная равна 3x²+ 24x + 45 = 3(x²+ 8x + 15).
Приравниваем её нулю (множитель в скобках):
x²+ 8x + 15 = 0.
Д = 64 - 4*1*15 = 4. х = (-8 +- 2)/2 = -3 и -5.
Находим знаки производной на полученных промежутках.
х = -6 -5 -4 -3 -1
y' = 9 0 -3 0 24.
Переход с + на - это максимум (х = -5, у = 0), с - на + это минимум(х = -3, у = -4). На промежутке (-∞; -5) и (-3; +∞) функция возрастает, на промежутке (-5; -3) функция убывает.
6. Найти интервалы выпуклости вверх и выпуклости вниз; определить точки перегиба
: y'' = (3x²+ 24x + 45)' = 6x + 24 = 6(x + 4) = 0.
Точка перегиба х = -4, у = -2.
Находим знаки второй производной на полученных промежутках.
x = -5 -4 -3
y'' = -6 0 6.
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый:
• Выпуклая на промежутке: (-∞; -4).
• Вогнутая на промежутке: (-4; +∞).
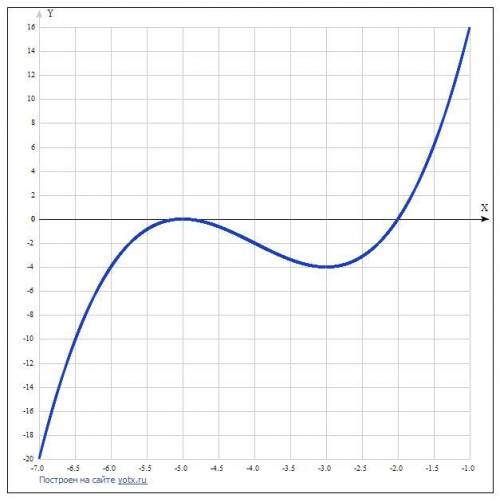
7. Построить график функции.
Таблица точек:
x y
-7.0 -20
-6.5 -10.1
-6.0 -4
-5.5 -0.9
-5.0 0
-4.5 -0.6
-4.0 -2
-3.5 -3.4
-3.0 -4
-2.5 -3.1
-2.0 0
-1.5 6.1
-1.0 16
График - в приложении.
 1. определить область существ" />
1. определить область существ" />
Рассмотрим данное неравенство
(7х + 2)/6 - х < (5х + 4)/3 - 4x
Перенесем все числа в левую часть уравнения.
(7х + 2)/6 - х - (5х + 4)/3 + 4x < 0
Приведем все числа и дроби к общему знаменателю 12.
(2(7х + 2) - 12х - 4(5х + 4) + 48х)/12 < 0
Раскроем скобки.
(14х + 4 - 12х - 20х - 16 + 48х)/12 < 0
Подведем подобные члены в скобках.
(30х -12)/12 < 0
Дробь меньше нуля когда или числитель или знаменатель отрицательный
Число 12 положительное, значит значение выражения (30х - 12) - отрицательно.
30х - 12 < 0
Отсюда: 30х < 12
Делим обе части неравенства на 30.
х < 12/30
Сократим дробь на 6.
х < 2/5
Отмечаем на числовой прямой число 2/5, обводим его в кружок (выкалываем точку), потому что неравенство строгое, число 2/5 не входит в промежуток.
Так как х < 2/5, штрихуем прямую левее числа 2/5.
Решением неравенства будет промежуток (- бесконечность; 2/5).
ответ: х принадлежит промежутку (- бесконечность; 2/5).