Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: айфон – деньги, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция y=f(x), это значит что каждому допустимому значению переменной x (которую называют «аргументом») соответствует одно значение переменной y (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» - не все можно подставить в зависимость.
Например, для функции y=x−−√ отрицательные значения аргумента x – недопустимы.
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида y=kx+b, где k и b – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения D(y) и область значений E(y).
Пошаговое объяснение:
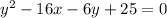
![\left[\begin{array}{ccc} 0&0\\0&1\\\end{array}\right]](/tpl/images/0459/2359/12771.png)
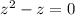
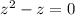
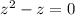
24-8=16
16+11=27часов