Для решения данной задачи нам необходимо определить вероятность того, что на четырех вынутых и расположенных в одну линию карточках можно будет прочесть слово "трос".
У нас дан набор из шести карточек с буквами: а, т, м, р, с, о. По условию карточки перемешаны, поэтому необходимо определить вероятность выбрать именно те карточки, которые позволят составить слово "трос".
Всего у нас шесть карточек, и мы выбираем четыре. В данной задаче порядок выбора карточек неважен, т.е. выбор карточек "а, т, р, с" будет считаться таким же результатом, как и выбор карточек "с, а, р, т". Поэтому для решения задачи нам необходимо определить количество благоприятных исходов и делить его на общее количество возможных исходов.
Чтобы получить слово "трос", мы должны выбрать одну карточку с буквой "т", одну карточку с буквой "р", одну карточку с буквой "о" и одну карточку с буквой "с".
Количество благоприятных исходов:
У нас есть шесть карточек и мы выбираем четыре. Для выбора карточки с буквой "т" у нас есть 1 благоприятный исход (только одна карточка с буквой "т"). Для выбора карточки с буквой "р" у нас также есть 1 благоприятный исход. Аналогично, для выбора карточек с буквами "о" и "с" у нас также есть по 1 благоприятному исходу.
Таким образом, общее количество благоприятных исходов равно 1 * 1 * 1 * 1 = 1.
Общее количество возможных исходов:
У нас есть шесть карточек и мы выбираем четыре. Для первой выбранной карточки у нас есть шесть вариантов выбора. Для второй выбранной карточки у нас уже будет пять вариантов выбора (уже одна карточка выбрана). Аналогично, для третьей и четвертой выбранных карточек у нас будет четыре и три варианта выбора соответственно.
Таким образом, общее количество возможных исходов равно 6 * 5 * 4 * 3 = 360.
Теперь можно определить вероятность того, что на четырех выбранных карточках можно будет прочесть слово "трос":
Вероятность = (количество благоприятных исходов) / (общее количество возможных исходов) = 1 / 360.
Таким образом, вероятность составить слово "трос" из четырех выбранных карточек равна 1/360.
(1) В данном случае, чтобы решить задачу, нам необходимо найти отношение, с которым плоскость сечения делит высоту пирамиды.
Площадь основания пирамиды равна 2916 дм², а площадь сечения равна 9 дм². По свойству подобных фигур площадь плоскостей, параллельных, пропорциональна квадратам соответствующих линейных размеров.
Это означает, что отношение площадей основания и сечения равно квадрату отношения линейных размеров основания и сечения.
Пусть x - это искомое отношение. Тогда x² = площадь основания / площадь сечения.
x² = 2916 / 9
x² = 324
x = √324
x = 18
Ответ: Плоскость сечения делит высоту пирамиды в отношении 18 : 1 (считая от вершины).
(2) Для решения этой задачи необходимо использовать ту же формулу о пропорциональности площадей плоскостей, параллельных.
Площадь основания пирамиды равна 363 дм², а плоскость сечения делит высоту пирамиды в отношении 3 : 8 (считая от вершины).
Пусть x - это площадь сечения. Тогда x = площадь основания * (3 / (3 + 8))²
x = 363 * (3 / 11)²
x = 363 * (3 / 121)
x = 9
-0.00428332 или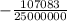
Пошаговое объяснение:
1) Проинтегрируем, используя метод подстановки:
2) Расставим значения:
3) Упростим выражение:
4) Вычислим: [Решение от lomaleks95]
Удачи!)