выразить в арах . а) 200м в квадрате, 205 метров в квадрате, 27м в квадрате, 40 м в квадрате.. б) 500 м в квадрате, 404 м в квадрате, 356 м в квадрате, , 150 м в квадрате. в) 3600 м в квадрате , 4 354 м в квадрате, 4 025 м в квадрате, , 7008 м в квадрате. г) 5000 м в квадрате, 2702 м в квадрате, 8030 м в квадрате, 6324 м в квадрате, , д) 3000м в квадрате, 6005м в квадрате, 3 м в квадрате, 80 м в квадрате .
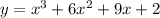
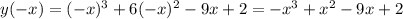 - не является ни четной, ни нечетной.
- не является ни четной, ни нечетной.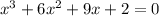
 - ноль функции
- ноль функции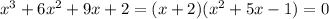
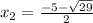 - ноль функции
- ноль функции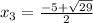 - ноль функции
- ноль функции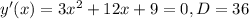
 - точка максимума
- точка максимума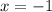 - точка минимума
- точка минимума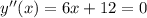

кроме х = -2.
2) Исследовать функцию на непрерывность - в точке х = -2 разрыв графика;
3) Определить, является ли данная функция четной, нечетной - подставим значение х = -х:
у(х)=(х^2-5)/(x+2).
у(-х)=(х^2-5)/(-x+2).
Функция не чётная и не нечётная.
4) Найти интервал возрастания и убывания функции и точки экстремума.
Производная равна y ' = (x²+4x+5)/(x+2)².
Приравняем 0: достаточно приравнять 0 числитель, знаменатель не может быть равен 0.
Выражение: x^2+4*x+5=0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=4^2-4*1*5=16-4*5=16-20=-4; Дискриминант меньше 0, уравнение не имеет корней.
Значит, у функции нет экстремумов.5) Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.
Находим вторую производную.
y '' = 2/(x+2)³.
Она не может быть равной 0. Перегибов нет.
Вторая производная при х < -2 отрицательна. График вогнут.
При х > -2 график выпуклый.
6) Найти асимптоты графика функции.
Горизонтальных асимптот нет.
Вертикальная х = -2.
Наклонные: для к находим предел f(x)/x к = 1.
для в находим предел f(x)-x в = -2.
Получаем уравнение у = х - 2.
Подробности в приложении.