Для того, чтобы найти точку максимума функции, сначала найдем ее производную (нужно знать, что , и ):Заметим, что производная (также, как и сама функция), не существует в точке (деление на ноль - "запрещенная операция").
Также, она обноляется в следующих двух точках:
Дальше можно все эти точки нанести на координатную прямую, и узнать знаки производной на соответствующих промежутках:
+ + + - - - - - - + + +
____________________________
Значит, точка максимума - это (так как знак сменяется с плюса на минус). В ней значение функции равно .
А точка минимума - это (минус меняется на плюс). В ней функция достигает значения .
Даны функции: 1) y = 6x^3 + 3x^2 2) y = (8/3x^3) - (3/2x^2) 3) y = 4x^2 - 3x.
1) y = 6x^3 + 3x^2. y' = 18x^2 + 6x = 0. 6x(3x + 1) = 0. x = 0. x = (-1/3). Имеем 3 промежутка На промежутках находят знаки производной (+ - больше нуля, - - меньше нуля). Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума. Находим знаки производной. x = -1 -0,33333 -0,2 0 1 y' = 12 0 -0,48 0 24. х = -1/3 это максимум, х = 0 это минимум.
2) y = (8/3x³) - (3/2x²) Приведём общему знаменателю. у = (16 - 9х)/6х³. y' = (-9*6x³ - 18x²(16 - 9x))/36x⁶ = (3x - 8)/x⁴. Приравниваем нулю числитель: 3х - 8 = 0, х = 8/3. Имеем один экстремум. x = 2 2,666667 3 y' = -0,125 0 0,012346. В точке х = 8/3 минимум.
3) y=4x^2-3x это уравнение параболы ветвями вверх. У неё один экстремум - в точке минимума Хо = -в/2а = 3/(2*4) = 3/8.
Для того, чтобы найти точку максимума функции, сначала найдем ее производную (нужно знать, что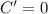
, 
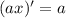и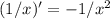 
):
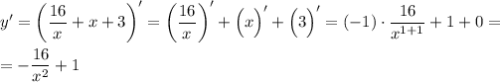Заметим, что производная (также, как и сама функция), не существует в точке 
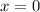(деление на ноль - "запрещенная операция").
Также, она обноляется в следующих двух точках:
Дальше можно все эти точки нанести на координатную прямую, и узнать знаки производной на соответствующих промежутках:
+ + + - - - - - - + + +
_______![\Big [ \; -4 \; \Big ]](/tpl/images/0857/2244/6eb69.png)
_______
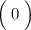_______![\Big [ \; 4 \; \Big ]](/tpl/images/0857/2244/02330.png)
_______ 
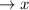
Значит, точка максимума - это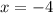
(так как знак сменяется с плюса на минус). В ней значение функции равно 
.
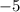А точка минимума - это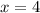
(минус меняется на плюс). В ней функция достигает значения 
.
ответ: - 4 .