
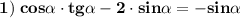
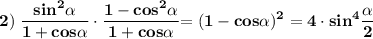
Пошаговое объяснение:
Известны тригонометрические тождества:
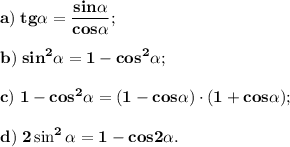
Решение.
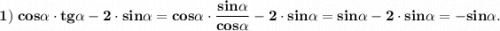
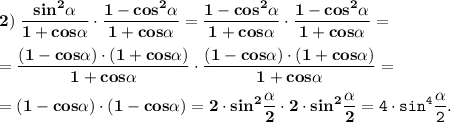
Старинная одежда русской знати по своему покрою в общем имела сходство с одеждой людей низшего класса, хотя сильно отличалась по качеству материала и отделке. Тело облегала широкая, не доходившая до колен рубаха из простого холста или шелка, смотря по достатку хозяина. У нарядной рубахи, обычно красного цвета, края и грудь вышивались золотом и шелками, вверху пристегивался серебряными или золотыми пуговицами богато украшенный воротник (он назывался «ожерельем»).
В простых, дешевых рубахах пуговицы были медными или заменялись запонками с петлями. Рубаха выпускалась поверх исподнего платья. На ноги надевались короткие порты или штаны без разреза, но с узлом, позволявшим стянуть или расширить их в поясе по желанию, и с карманами (зепью). Штаны шились из тафты, шелка, сукна, а также из грубой шерстяной ткани или холста.
>. потому что 26+8=34,а 26-8=18
значит 34>18
Пошаговое объяснение:
если число в модуле, | - этот знак значит модуль
число в этих палках называется модулем.Модуль чтсла всегда будет равен положительному числу. т.е |-24|=24
так работает модуль
важный факт: если положительно число будет находиться в модуле,оно не изменится , т.е |25|=25
значит наш пример |26|+|8| тоже самое,что и пример без этих палок
но вот пример справа: если отрицательное число находится в модуле,то оно изменитя,но если весь пример находится в модуле,то он решается как обычный.Т.е можно сказать,что это задание так же можно было бы и записать как |26|+|-8|>|18|
выходит тоже самое
попробовал объяснить тему "модули."
у меня получилось? кто то хоть что нибудь понял?
поставь лайк и отметь ответ на 5 звезд)
если поставишь 5 звезд,то в мире будет счастлив один енотик))
Пошаговое объяснение:
1) Упростим выражение
Воспользуемся формулой
2) Упростим выражение
Представим по основному тригонометрическому тождеству
и разложим на множители, применяя формулу сокращенного умножения