Максимально возможная суммарная площадь обзора
Sобщ.=216.6046 ед.²
Пошаговое объяснение:
Поскольку в задании чётко не ограничен минимальный радиус обзора охотников, то примем его за 0 (охотник уснул).
Площадь обзора каждого из охотников представляет собой круг.
Формула площади круга:
S=πR².
Как видно из формулы площади круга, зависимость от радиуса обзора - квадратичная. Это говорит о том, что для получения максимальной площади обзора, лучше получить один максимально большой круг и два оставшихся небольших, чем два одинаковых и один поменьше или три примерно одинаковых круга. Справедливость этого утверждения подтверждает форма графика квадратичной параболы, и понимание того, что при суммировании площадей мы выполняем "линейную" операцию.
Для того, чтобы определить максимальный круг обзора, нам нужно вычислить расстояния между точками, в которых расположены охотники. Для удобства обозначим точки буквами А(4;9), В(5;1); С(12;7).
Найдем АВ: 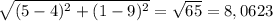
Найдем АС: 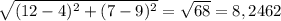
Найдем ВС: 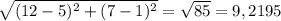
Значит "отдаем приоритет" охотнику в точке С, т.к. два самых длинных расстояния АС и ВС связаны с этой точкой. Охотника в точке А - "усыпляем", т.е. даём ему радиус обзора, равный 0, при этом он вырождается в точку с площадью, равной нулю.
Радиус обзора охотника в точке С принимаем равным АС, иначе если его принять бОльшим, то в площадь обзора включится точка А, что равносильно пересечению участков охотников.
Тогда получаем три площади обзора с радиусами:
0; АС; (ВС-АС)
Вычислим эти площади.
Для точки А: Sa=0 ед.²
Для точки С: Sc=π*АС²=213,6283 ед.²
Для точки В: Sb=π*(BC-АС)²=2.9763 ед.²
Sобщ.=0+213,6283+2,9763=216.6046 ед.²
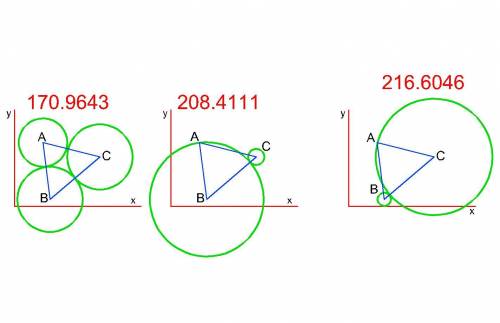
На рисунке прилагаю 3 возможных варианта обзоров охотников из которых только последний (крайний справа) - правильный.
Максимально возможная суммарная площадь обзора
Sобщ.=216.6046 ед.²
Пошаговое объяснение:
Поскольку в задании чётко не ограничен минимальный радиус обзора охотников, то примем его за 0 (охотник уснул).
Площадь обзора каждого из охотников представляет собой круг.
Формула площади круга:
S=πR².
Как видно из формулы площади круга, зависимость от радиуса обзора - квадратичная. Это говорит о том, что для получения максимальной площади обзора, лучше получить один максимально большой круг и два оставшихся небольших, чем два одинаковых и один поменьше или три примерно одинаковых круга. Справедливость этого утверждения подтверждает форма графика квадратичной параболы, и понимание того, что при суммировании площадей мы выполняем "линейную" операцию.
Для того, чтобы определить максимальный круг обзора, нам нужно вычислить расстояния между точками, в которых расположены охотники. Для удобства обозначим точки буквами А(4;9), В(5;1); С(12;7).
Найдем АВ: 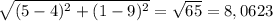
Найдем АС: 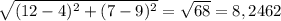
Найдем ВС: 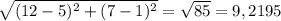
Значит "отдаем приоритет" охотнику в точке С, т.к. два самых длинных расстояния АС и ВС связаны с этой точкой. Охотника в точке А - "усыпляем", т.е. даём ему радиус обзора, равный 0, при этом он вырождается в точку с площадью, равной нулю.
Радиус обзора охотника в точке С принимаем равным АС, иначе если его принять бОльшим, то в площадь обзора включится точка А, что равносильно пересечению участков охотников.
Тогда получаем три площади обзора с радиусами:
0; АС; (ВС-АС)
Вычислим эти площади.
Для точки А: Sa=0 ед.²
Для точки С: Sc=π*АС²=213,6283 ед.²
Для точки В: Sb=π*(BC-АС)²=2.9763 ед.²
Sобщ.=0+213,6283+2,9763=216.6046 ед.²
На рисунке прилагаю 3 возможных варианта обзоров охотников из которых только последний (крайний справа) - правильный.

1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Приемлемо, однако следует добавить, что эти три точки не лежат на одной прямой.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Это неверно. И медианой, и высотой является только биссектрисса угла, противолежащего основанию, а не любая.
3. Площадь любого треугольника можно вычислить по формулам:
Верно.
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле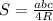 , где радиус этой окружности вычисляется по теореме косинусов:
, где радиус этой окружности вычисляется по теореме косинусов: 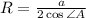 .
.
Неверно. Речь идет про описанную окружность, а не вписаную.
5. А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула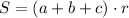
Здесь так же перепутаны вписанная и описанная окружности. Речь идет про вписанную окружности. К тому же ее радиус вычисляется по теореме синусов, а не косинусов.
6. Прямая, параллельная стороне треугольника, является его средней линией.
Неверно. Не всякая прямая, паралельная стороне треугольника является его средней линией. Можно дополнить тем, что прямая проходит через середину другой стороны, тогда это будет средняя линия.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
В тексте приведен признак подобия треугольников, но не равенства. Не все прямоугольные треугольники подобны. Для подобия двух прямоугольных треугольников достаточно чтобы были равны два острых угла.
Исправленный вариантТреугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками, не лежащими на одной прямой.
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести биссектрису угла, противолежащего основанию, она будет являться медианой и высотой.
Площадь любого треугольника можно вычислить по формулам:
Если около треугольника описана окружность, то его площадь можно найти по формуле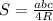 , где радиус этой окружности вычисляется по теореме синусов:
, где радиус этой окружности вычисляется по теореме синусов: 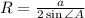
А если в треугольник вписать окружность, то для нахождения площади треугольника справедлива формула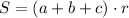 .
.
Прямая, параллельная стороне треугольника и проходящая через его середину, является его средней линией.
Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники подобны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники с парой равных острых углов подобны.