Question

В 3 из 10 составленных бухгалтером отчетах имеются ошибки. Ревизор решил проверить наудачу 6 отчетов. Какова вероятность, что а) ошибки не будут обнаружены; б) будет обнаружена хотя бы одна ошибка.

Answer 1

а) ошибки не будут обнаружены;    вероятность = 1/30

б) будет обнаружена хотя бы одна ошибка  вероятность = 29/30

Пошаговое объяснение:

Наше событие

А = {из 6 выбранных отчетов хотя бы одна ошибка }

Противоположное событие

$\overline A$ = { из 6 выбранных отчетов ни одной ошибки} =

   = {все 6 отчетов верные} =

   = { ошибки не будут обнаружены }

Запишем вероятность события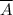 $\overline A$ по формуле классического определения вероятности.

Общее число исходов

$\displaystyle n= C_{10}^6=\frac{10!}{6!(10-6)!} =\frac{7*8*9*10}{2*3*4} =210$

Благоприятное число исходов (выбрать 6 правильных отчетов из 7 правильных)

$\displaystyle n= C_{7}^6=\frac{7!}{6!(7-6)!} =7$

Таким образом вероятность того, что все 6 отчетов будут верные, т.е.

а) ошибки не будут обнаружены

$\displaystyle P(\overline A)= \frac{7}{210} =\frac{1}{30}$

б)  будет обнаружена хотя бы одна ошибка

$\displaystyle P(A) = 1-P(\overline A)=1-\frac{1}{30} =\frac{29}{30}$

#SPJ1