Question

Знайдіть найбільше і найменше значення функції на відрізку [а, б]

Answer 1

Найти наибольшее и наименьшее значение функции y=x^3-3x^2-9x+35 на промежутке [-4;4].

ответ:

Наибольшее значение функции на промежутке [-4;4] - y(-1)=40; наименьшее - у=(-4)=(-41).

Пошаговое объяснение:

Для начала вспомним теорию. Алгоритм нахождения наибольшего и наименьшего значений функции на заданном промежутке:

Найти производную ф-ции. Находим критические точки, которые принадлежат заданному промежутку.Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.Выбираем наибольшее и наименьшее из них.1. Найдём производную функции.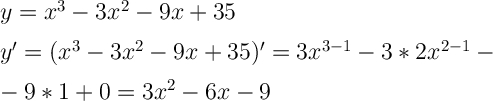

$\Large \boldsymbol {} y=x^3-3x^2-9x+35y'=(x^3-3x^2-9x+35)'=3x^{3-1}-3*2x^{2-1}--9*1+0=3x^2-6x-9$

2. Находим критические точки, которые принадлежат заданному промежутку.

$\Large \boldsymbol {} x\inx\in(-\infty;+\infty)3x^2-6x-9=0D=b^2-4ac=(-6)^2-4*3*(-9)=36+108=144x_{1,2}=\frac{-b\pm\sqrt{D} }{2a} x_1=\frac{-(-6)+\sqrt{144} }{2*3} =\frac{6+12}{6} =\frac{18}{6} =3\in[4;4]x_2=\frac{-(-6)-\sqrt{144} }{2*3} =\frac{6-12}{6} =\frac{-6}{6} =-1\in[4;4]$

3. Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.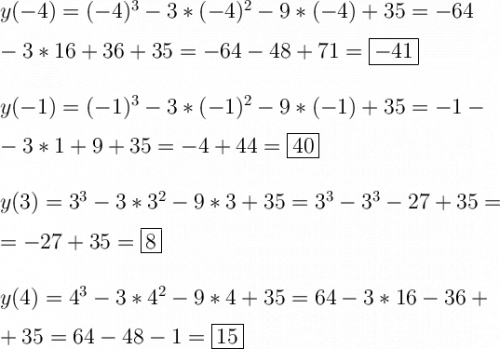

$\Large \boldsymbol {} y(-4)=(-4)^3-3*(-4)^2-9*(-4)+35=-64-3*16+36+35=-64-48+71=\boxed{-41}y(-1)=(-1)^3-3*(-1)^2-9*(-1)+35=-1--3*1+9+35=-4+44=\boxed{40}y(3)=3^3-3*3^2-9*3+35=3^3-3^3-27+35==-27+35=\boxed{8}y(4)=4^3-3*4^2-9*4+35=64-3*16-36++35=64-48-1=\boxed{15}$

4. Выбираем наибольшее и наименьшее из получившихся значений:

$\Large \boldsymbol {} max \:y(x)=y(-1)=40 \:\:\:\:\:\:\:\:\:\:\:\min \:y(x)=y(-4)=-41\\ \ [-4;4] \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:[-4;4]$