300.
Пошаговое объяснение:
Пусть ВС = 20 - большая сторона прямоугольника АВСД, тогда АВ - меньшая сторона.
Обозначим ВК = 12 - расстояние от вершины В до диагонали АС .
ΔВСК - прямоугольный с гипотенузой ВС и катетами ВК м СК.
найдём СК, используя теорему Пифагора:
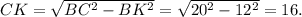
Рассмотрим два прямоугольных треугольника: ΔВСК и ΔАВК.
Эти треугольники подобны, так как ∠ВСК = ∠АВК как углы с взаимно перпендикулярными сторонами (ВС ⊥ АВ и АК ⊥ ВК).
В подобных треугольниках соответственные стороны пропорциональна, поэтому
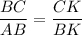
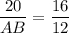
АВ · 16 = 20 · 12
16 АВ = 240
АВ = 240 : 16
АВ = 15.
Площадь прямоугольника равна произведению смежных сторон:
S = AB · BC = 15 · 20 = 300.
4, 64.
Пошаговое объяснение:
Очевидно, арифметические прогрессии с разными разностями не могут содержать больше, чем одно общее число.
Второе наблюдение: непостоянная арифметическая прогрессия и геометрическая прогрессия не могут иметь больше двух общих членов.
Действительно, пусть x - d, x и x + d - геометрическая прогрессия (это арифметическая прогрессия по построению). Тогда
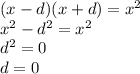
Если бы у арифметических прогрессий был бы общий член, то любая другая подпоследовательность длины 4 содержала бы как минимум 3 члена одной из этих прогрессий. Значит, арифметические прогрессии не имеют общих членов.
Остается два варианта:
1) Последовательность: x - 12, x - 8, x - 4, x, y, y + 16, y + 32, y + 48.
Геометрическая прогрессия: x - 4, x, y, y + 16. Условие того, что это геометрическая прогрессия:
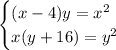
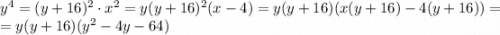
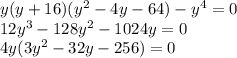
Корень первого сомножителя y = 0. Ищем корни скобки:
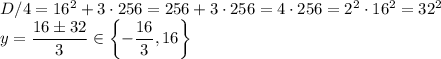
Итак, y = -16/3, 0 и 16. Им соответствуют
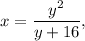
x = 8/3, x = 0 и x = 8, соответственно. Первые два варианта не подходят, при этом последовательность не получается возрастающей. Остается единственный вариант: x = 8, y = 16. Тогда последовательность имеет вид:
-4, 0, 4, 8, 16, 32, 48, 64.
2) Последовательность: x - 48, x - 32, x - 16, x, y, y + 4, y + 8, y + 12.
Геометрическая прогрессия: x - 16, x, y, y + 4. Условие того, что это геометрическая прогрессия:
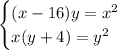
Заметим, что если поменять x на -y, а y на -x, то получится точно такая же система, что и в первом случае. Тогда и решения её известны: (-16, -8), (0, 0) и (16/3, -8/3).
Вновь только первое решение соответствует возрастающей последовательности:
-64, -48, -32, -16, -8, -4, 0, 4.
рассмотрим четырехугольник ABCD. угол А-90 по условию. СH-высота. значит угол H-90. угол B-тоже 90 т.к. трапеция прямоугольная. зн. угол BCH - тоже 90(360-(90+90+90)=90). зн. этот четырехугольник - прямоугольник т.к. у прямоугольника все углы по 90. BC параллельна AD и секущей AC. угол АCH- 45(как накрестлежащий при вышесказанных параллельных). рассмотрим треугольник ACD. угол САН - 45(т.к. угол А -90 а угол САВ - 45. зн. 90-45=45) угол D=45. по вычислению(360 - (90+90+135). зн. этогт треугольник равнобедренный. а в равнобедренном треуг. биссекктриса - медиана и высота. зн. АН=НD=15.Теперь рассмотрим треуг АВС и треуг. АНС. они равны по катету и гипотенузе(гипотенуза - общая а в прямоугольнике противоположные стороны равны. тоесть АН=ВС=15). значит этот четырехугольник - квадрат. значит все стороны равны значит наименьшая боковая сторона равна 15. вроде так)))
Пошаговое объяснение:
Площадь прямоугольника АВСD равна 320 ед²
Пошаговое объяснение:
Площадь прямоугольника равна произведению его длины на ширину:
S = AB*BCВН⊥АС, ВН - Расстояние от вершины В до диагонали АС. ВН = 12.
1) ΔВНС (∠Н=90°)
По теореме Пифагора находим катет НС:
НС² = ВС²-ВН²=20²-12²=400-144=256
НС=√256 = 16 ед
2) ΔАВС (∠В=90°)
Высота, которую провели из прямого угла на гипотенузу треугольника, численно равна среднему геометрическому проекций обоих катетов на эту гипотенузу:
ВН²=АН*НС
Тогда АС= АН+НС = 9+16 = 25 ед
3) По теореме Пифагора находим катет АВ в прямоугольном ΔАВС:
АВ² = АС²-ВС² = 25²-20² = 625-400 = 225
АВ = √225 = 15 ед
4) Площадь АВСD:
S = 15*20 = 320 ед