Question

M(1;-5), L: 3x+3y+2=0. Напишите уравнение прямых проходящих через точку М одна из которых паралельна, а другая - перпендикулярная прямой L

Answer 1

L1: y = -x-4
L2: y = x-6

Пошаговое объяснение:

Дано:
M(1;-5)
L: 3x+3y+2 = 0

Найти: L1, L2

Решение: 1) Для начала выразим прямую L как каноническое уравнение прямой y = kx+b
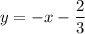
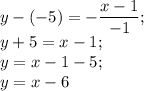
3x+3y+2 = 0;
3y = -3x-2|:3;
$\displaystyle y=-x-\frac{2}{3}$
2) Прямые параллельны когда у них меняется свободный член, т.е. k остаётся неизменным, а b нет. Получается коэффициент k у параллельной прямой будет также равен -1
Подставим координаты точки М в каноническое уравнение прямой
-5 = -1*1+b
b = -5+1
b = -4
Уравнение параллельной 3x+3y+2 = 0 прямой, проходящей через точку M(1;-5) будет выглядеть как y = -x-4
3) Для перпендикулярной y = kx+b прямой, проходящей через точку N(x₁,y₁) есть следующая формула:
y-y₁ = -(x-x₁)/k
Получается, перпендикулярная y = -x-²/₃ прямая, проходящая через M(1;-5) будет выглядеть как:
$\displaystyle y-(-5) = -\frac{x-1}{-1} ;\\y+5 = x-1;\\y = x-1-5;\\y=x-6$

Если построить все данные в одной плоскости, то можно убедиться в правильном нахождении неизвестных прямых(см. вложение)