
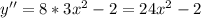
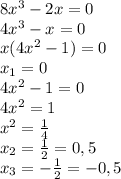
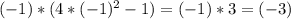 - знак минус
- знак минус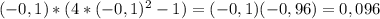 - знак плюс
- знак плюс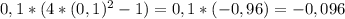 - знак минус
- знак минус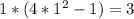 - знак плюс
- знак плюс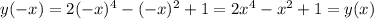 - значит функция четная
- значит функция четная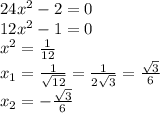
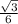 ≈0,289
≈0,289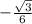 ≈-0,289
≈-0,289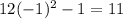 - знак плюс
- знак плюс![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/a1cfa.png) и
и 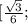 ;+oo)
;+oo)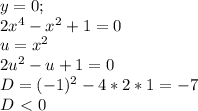
![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4016/a1cfa.png) и
и 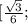 ;+oo)
;+oo)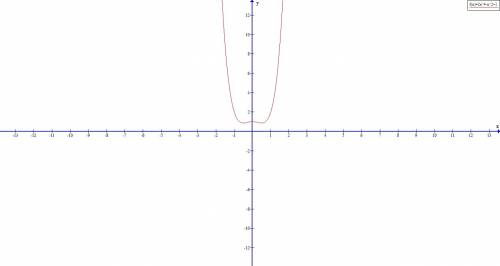
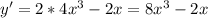
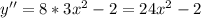
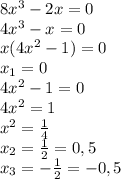
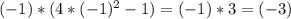 - знак минус
- знак минус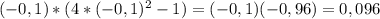 - знак плюс
- знак плюс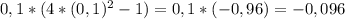 - знак минус
- знак минус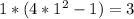 - знак плюс
- знак плюс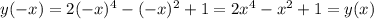 - значит функция четная
- значит функция четная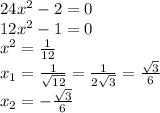
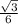 ≈0,289
≈0,289 ≈-0,289
≈-0,289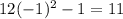 - знак плюс
- знак плюс![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/a1cfa.png) и
и 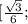 ;+oo)
;+oo)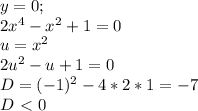
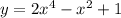
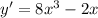
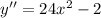
![[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/e2f5f.png)
![-\frac{\sqrt{3}}{6 }]](/tpl/images/0773/4085/a1cfa.png) и
и 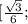 ;+oo)
;+oo)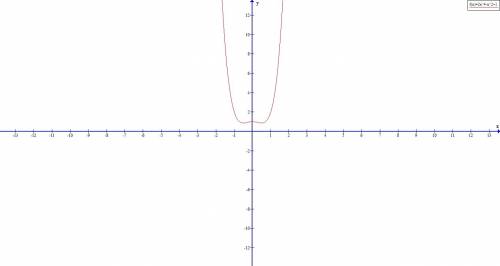
ответ
Начнём с того что обозначим через (х) как 1 кг авокадо
На 7кг авокадо не хватает 500 рублей, значит (7х-500)
И также обозначим 4кг авокадо (4х + 400) так как осталось 400 рублей
Теперь можно составить уравнение
↓ ↓
7х - 500 = 4х + 400
7х - 4 х = 500 + 400
3х = 900
х = 900 ÷ 3
х = 300 ( рублей )
В итоге мы получили ответ, что 1 кг авокадо стоит 300 рублей